03. Потенциал. Энергия системы электрических зарядов. Работа по перемещению заряда в поле
ФОРМУЛЫ.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду;
= П/Q,
или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:
= A/Q.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Отметим, что при перемещении заряда в электрическом поле работа Aв.с внешних сил равна по модулю работе Aс.п сил поля и противоположна ей по знаку:
Aв.с = – Aс.п.
Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянии r от заряда,
.
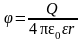Потенциал электрического поля, создаваемого металлической, несущей заряд Q сферой радиусом R, на расстоянии гот центра сферы:
внутри сферы (r < R)
;
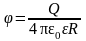на поверхности сферы (r = R)
;
вне сферы (r > R)
.
Во всех приведенных для потенциала заряженной сферы формулах есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, созданного системой п точечных зарядов, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраической сумме потенциалов 1, 2, ... , n, создаваемых отдельными точечными зарядами Q1, Q2, ..., Qn:
.
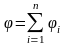Энергия W взаимодействия системы точечных зарядов Q1, Q2, ..., Qn определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
,
здесь i – потенциал поля, создаваемого всеми п – 1 зарядами (за исключением 1-го) в точке, здесь расположен заряд Qi.
Потенциал связан с напряженностью электрического поля соотношением
=
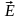–grad.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
,
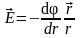или в скалярной форме
,
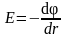а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению,
E = (1 – 2)/d,
здесь 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2,
A
=
Q(1
–
2),
или
,
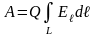здесь Eℓ – проекция вектора напряженности Е на направление перемещения; dℓ – перемещение.
В случае однородного поля последняя формула принимает вид
A = QEℓcos,
здесь ℓ – перемещение; – угол между направлениями вектора Е и перемещения ℓ.
ЗАДАЧИ
03.01. Потенциальная энергия и потенциал поля точечных зарядов (Потенциал точечных зарядов)
Уровень 1.
1. Чему равна энергия (в мДж) взаимодействия точечных зарядов 2 мкКл и 4 мкКл, находящихся на расстоянии 30 см друг от друга? k=9·109 м/Ф. [240]
2. Чему равна энергия (в мДж) взаимодействия системы трех зарядов 2, –1 и 3 мкКл, расположенных в вершинах равностороннего треугольника со стороной 10 см? k=9·109 м/Ф. [90]
3. Точечный заряд Q=10 нКл, находясь в некоторой точке поля, обладает потенциальной энергией П=10 мкДж. Найти потенциал φ этой точки поля. [1000]
4. При перемещении заряда Q=20 нКл между двумя точками поля внешними силами была совершена работа А=4 мкДж. Определить разность Δφ потенциалов этих точек поля. [200]
5. Поле создано точечным зарядом Q=1 нКл. Определить потенциал φ поля в точке, удаленной от заряда на расстояние r=20 см. 1/(4π0)=9·109 м/Ф. [45]
6. Вычислить потенциальную энергию П системы двух точечных зарядов Q1=100 нКл и Q2=10 нКл, находящихся на расстоянии d=10 см друг от друга. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 106. [90]
Уровень 2.
1. Чему равна энергия (в мДж) взаимодействия системы трех зарядов 2, 1 и 3 мкКл, расположенных в указанном порядке вдоль прямой линии, если расстояние между соседними зарядами равно 30 см? k=9·109 м/Ф. [240]
2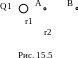
.
Найдите энергию (в мДж) взаимодействия
системы четырех зарядов 1, 2, 3 и 4 мкКл,
расположенных в вершинах правильного
тетраэдра с ребром 50 см. k=9·109
м/Ф. [630]
3
.
Электрическое поле создано точечным
положительным зарядом Q1=6
нКл. Положительный заряд Q2
переносится из точки А
этого
поля в точку В
(рис.
15.5). Каково изменение потенциальной
энергии ΔП, приходящееся на единицу
переносимого заряда, если r1=20
см и r2=50
см? 1/(4π0)=9·109
м/Ф. [162]
4. Электрическое поле создано точечным зарядом Q1=50 нКл. Определить изменение ΔП потенциальной энергии системы зарядов при перемещении точечного заряда Q2=–2 нКл из точки С в точку В (рис. 15.6), если r1=10 см, r2=20 см. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 108. [450]
5. Определить потенциал φ электрического поля в точке, удаленной от зарядов Q1=–0,2 мкКл и Q2=0,5 мкКл соответственно на r1=15 см и r2=25 см. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 10–6. [6]
6. Заряды Q1=1 мкКл и Q2=–1 мкКл находятся на расстоянии d=10 см. Определить потенциал φ поля в точке, удаленной на расстояние r=10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно направлению от Q1 к Q2. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 10–3 и округлите до целого значения. [26] [27]
7. Найти потенциальную энергию П системы трех точечных зарядов Q1=10 нКл, Q2=20 нКл и Q3=–30 нКл, расположенных в вершинах равностороннего треугольника со стороной длиной a=10 см. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 106. [63]
8
.
На расстоянии ℓ=50
см
от
точечного заряда q=20
нКл находится центр проводящего шара
радиуса R=10
см. Определить потенциал φ шара, если
на нем распределен заряд Q=6
нКл. 1/(4π0)=9·109
м/Ф. [900]
9. Четыре электрона и протон расположены так, как это указано на рисунке 15.19. Определить потенциальную энергию П такой системы зарядов (в ДЖ и эВ). При расчетах принять a=0,3 нм. 1/(4π0)=9·109 м/Ф. 1) Ответ в Дж умножьте на 1021 и округлите до целого значения. 2) Ответ в эВ умножьте на 102 и округлите до целого значения.
1) [186] [187] 2) [116] [117]
Уровень 3.
1. Четыре одинаковых заряда 2 мкКл расположены на прямой линии. Расстояние между соседними зарядами равно 60 см. Какую надо совершить работу (в мДж), чтобы разместить эти заряды в вершинах правильного тетраэдра с ребром 60 см? [100]
2. В вершинах острых углов ромба закреплены заряды 7 нКл, а в вершинах тупых углов находятся две частицы массой 2 мг и зарядом 2 нКл каждая. Частицы одновременно отпускают, и они приходят в движение. Чему будет равна скорость частиц после их разлета на большое расстояние? Сторона ромба 3 см, а его острый угол 60°. k=9·109 м/Ф. [3]
3. В одной вершине равностороннего треугольника со стороной 2 см закреплен точечный заряд 40 нКл, а в двух других находятся частицы массой 5 мг и зарядом 10 нКл каждая. Частицы отпускают, и они приходят в движение. Чему будет равна их скорость на большом расстоянии от заряда? k=9·109 м/Ф. [9]
4. Три одинаковых шарика, несущие одинаковый заряд 2 мкКл, соединены попарно тремя одинаковыми пружинами и удерживаются на расстоянии 5 см друг от друга. Шарики отпускают, и они приходят в движение. Найдите жесткость каждой пружины, если в начальном положении они не деформированы, а максимальное расстояние между шариками в процессе движения в три раза больше начального. k=9·109 м/Ф. [96]
5. Какова потенциальная энергия П системы четырех одинаковых точечных зарядов Q=10 нКл, расположенных в вершинах квадрата со стороной длиной а=10 см? 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 106 и округлите до целого значения. [49] [48]
6. Определить потенциальную энергию П системы четырех точечных зарядов, расположенных в вершинах квадрата со стороной длиной a=10 см. Заряды одинаковы по модулю Q=10 нКл, но два из них отрицательны. Рассмотреть два возможных случая расположения зарядов: 1) одноименные заряды расположены в противоположных вершинах квадрата, 2) одноименные заряды расположены на одной стороне квадрата. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 106 и округлите до целого значения.
1) [23] [24] 2) [13] [12]
7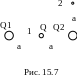
.
Система состоит из трех зарядов – двух
одинаковых по величине Q1=|Q2|=1
мкКл и противоположных по знаку и заряда
Q=20
нКл,
расположенного точке 1 посередине между
двумя другими зарядами системы (рис.
15.7). Определить изменение потенциальной
энергии ΔП системы при переносе заряда
Q
из точки 1 в точку 2. Эти точки удалены
от отрицательного заряда Q1
на расстояние а=0,2
м.
1/(4π0)=9·109
м/Ф. Полученный ответ умножьте на 106
и округлите до целого значения. [498] [497]
8. Три протона удерживается в вершинах равностороннего треугольника со стороной a=0,3–15 м. При освобождении протонов от удерживающих их связей, они разлетаются под действием сил отталкивания. Определить скорости υ протонов на достаточно большом расстоянии ℓ (ℓ>>a). Заряд протона e=1,6·10–19 Кл, масса протона m=1,67·10–27 кг. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 10–5 и округлите до целого значения. [166] [167]
Уровень 4.
1. Два небольших тела массой 5 г каждое, заряженные одинаковым зарядом 1 мкКл, находятся на горизонтальной плоскости на расстоянии 10 м друг от друга. Коэффициент трения тел о плоскость равен 0,5. Какую минимальную начальную скорость надо сообщить одному из тел, чтобы сдвинуть с места второе тело? k=9·109 м/Ф, g=10 м/с2. [8]
2. Два небольших тела массой 100 г каждое, несущие заряды 10 мкКл, удерживают на горизонтальной плоскости на расстоянии 1 м друг от друга. Коэффициент трения тел о плоскость 0,1. Тела одновременно освобождают. Найдите максимальную скорость тел в процессе движения, k=9·109 м/Ф, g=10 м/с2. [2]
3. Два маленьких шарика массой 150 г, лежащие на гладкой горизонтальной плоскости, соединены недеформированной пружиной длиной 40 см и жесткостью 10 Н/м. После сообщения шарикам зарядов одного знака длина пружины стала равна 80 см. Какую минимальную одинаковую скорость надо сообщить шарикам навстречу друг другу, чтобы они сблизились до прежнего расстояния? [4]
4. На высоте 3 м над землей закреплен заряд –4 мкКл, а под ним на высоте 2,2 м находится частица массой 0,9 г с зарядом 1 мкКл. Какую скорость надо сообщить частице вертикально вниз, чтобы она достигла поверхности земли? k=9·109 м/Ф, g=10 м/с2. [6]
5. На расстоянии 1 м от закрепленного заряда –100 нКл расположена частица массой 0,1 г с зарядом 2 мкКл. Заряды находятся в однородном внешнем поле, напряженность которого равна 100 В/м и направлена от отрицательного заряда к положительному. Какую минимальную скорость надо сообщить частице в направлении силовых линий, чтобы она улетела на бесконечность? k=9·109 м/Ф. Силу тяжести не учитывать. [4]
6. Две частицы, имеющие массы 2 и 3 г и заряды 3 и –12 мкКл, удаляются друг от друга. В некоторый момент они находятся на расстоянии 10 м и имеют одинаковые скорости 3 м/с. Найдите наибольшее расстояние между частицами в процессе движения. k=9·109 м/Ф. [30]
7. Две частицы имеют массу 1 г каждая и заряды 1 и –1 мкКл. В начальный момент расстояние между частицами 3,2 м, одна из частиц покоится, а другая удаляется от нее со скоростью 3 м/с. Найдите максимальное расстояние между частицами в процессе движения, k=9·109 м/Ф. [16]
8. Две частицы имеют массы 4 и 5 г и заряды 1 и –1 мкКл. В начальный момент расстояние между частицами 10 см, первая частица неподвижна, а вторая удаляется от нее со скоростью ʋ. При каком минимальном значении ʋ эта частица не столкнется с первой частицей? k=9·109 м/Ф. [9]
9. Два диэлектрических шара равномерно заряжены одинаковым зарядом 3 мкКл. Масса первого шара 6 г, масса второго 12 г, радиус каждого шара 1 см. Вначале шары удерживают так, что они касаются друг друга, а затем отпускают. Найдите конечную скорость первого шара, k=9·109 м/Ф. [30]
10. Два диэлектрических шара равномерно заряжены по объему, первый – зарядом 1 мкКл, второй – зарядом 0,6 мкКл. Масса первого шара 6 г, второго – 4 г, радиус каждого шара 1 см. Вначале первый шар покоится, а второй издалека приближается к нему со скоростью ʋ. При каком минимальном значении ʋ шары коснутся друг друга? k=9·109 м/Ф. [15]
11. Два диэлектрических шара радиусом 1 см каждый равномерно заряжены одинаковым зарядом 0,4 мкКл. В начальный момент один из шаров массой 16 г покоится, а второй массой 8 г издалека приближается к нему со скоростью 6 м/с. Найдите скорость первоначально покоившегося шара сразу после их соударения, считая его абсолютно упругим. k=9·109 м/Ф. [3]
03.02. Потенциал поля линейного распределенных зарядов (Потенциал линейного заряда)
Уровень 3.
1. По тонкому кольцу радиусом R=10 см равномерно распределен заряд с линейной плотностью τ=10 нКл/м. Определить потенциал φ в точке, лежащей на оси кольца, на расстоянии а=5 см от центра. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [505] [506]
Уровень 5 (Интегрирование).
1. На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью τ=10 нКл/м. Вычислить потенциал φ, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка. 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения. [62] [63]
2. Тонкий стержень длиной ℓ=10 см несет равномерно распределенный заряд Q=1 нКл. Определить потенциал τ электрического поля в точке, лежащей на оси стержня на расстоянии а=20 см от ближайшего его конца. 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения. [36] [37]
3. Тонкие стержни образуют квадрат со стороной длиной а. Стержни заряжены с линейной плотностью τ=1,33 нКл/м. Найти потенциал φ в центре квадрата. 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения. [84] [85]
4. Бесконечно длинная тонкая прямая нить несет равномерно распределенный по длине нити заряд с линейной плотностью τ=0,01 мкКл/м. Определить разность потенциалов Δφ двух точек поля, удаленных от нити на r1=2 см и r2=4 см. 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения. [125] [124]
03.03. Потенциал поля зарядов, распределенных по поверхности (Потенциал поверхностного заряда)
Уровень 1.
1. Уединенный металлический шар радиусом R=10 см можно зарядить до некоторого максимального заряда, при этом заряде напряженность Е поля, при которой происходит пробой воздуха, равна 3 МВ/м. Найти максимальную поверхностную плотность σ электрических зарядов перед пробоем. 0=8,85·10–12 Ф/м. Полученный ответ умножьте на 106 и округлите до целого значения. [27] [26]
Уровень 2.
1. Заряд распределен равномерно по бесконечной плоскости с поверхностной плотностью σ=10 нКл/м2. Определить; разность потенциалов Δφ двух точек поля, одна из которых находится на плоскости, а другая удалена от плоскости на расстояние d=10 см. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [56] [57]
2. Две бесконечные параллельные плоскости находятся на расстоянии d=0,5 см друг от друга. На плоскостях равномерно распределены заряды с поверхностными плотностями σ1=0,2мкKл/м2 и σ2=–0,3 мкКл/м2. Определить разность потенциалов U между плоскостями. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [141] [142]
3. Две бесконечные параллельные плоскости находятся на расстоянии d=1 см друг от друга. Плоскости несут равномерно распределенные по поверхностям заряды с плотностями σ1=0,2 мкКл/м2 и σ2=0,5 мкКл/м2. Найти разность потенциалов U пластин. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [169] [170]
4. Металлический шарик диаметром d=2 см заряжен отрицательно до потенциала φ=150 В. Сколько электронов находится на поверхности шарика? Заряд электрона e=1,6·10–19 Кл. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 10–7 и округлите до целого значения. [104] [105]
5
.
Электрическое поле создано отрицательно
заряженным металлическим шаром.
Определить работу A1,2
внешних
сил по перемещению заряда Q=40
нКл
из точки 1 с потенциалом φ1=–300
В в точку 2 (рис. 15.9). Полученный ответ
умножьте на 106.
[6]
Уровень 3.
1. Металлический шар радиусом R1=10 cм заряжен до потенциала φ1=300 В. Определить потенциал φ2 этого шара в двух случаях: 1) после того, как его окружат сферической проводящей оболочкой радиусом R2=15 см и на короткое время соединят с ней проводником; 2) если его окружить сферической проводящей заземленной оболочкой с R2=15 см.
1) [200] 2) [100]
2. Определить потенциал φ, до которого можно зарядить уединенный металлический шар радиусом R=10 см, если напряженность Е поля, при которой происходит пробой воздуха, равна 3 МВ/м. Полученный ответ умножьте на 10–3. [300]
3. Сто одинаковых капель ртути, заряженных до потенциала φ=20 В, сливаются в одну каплю. Каков потенциал φ1 образовавшейся капли? Полученный ответ округлите до целого значения. [431] [430]
Уровень 4.
1. Имеются две концентрические металлические сферы радиусами R1=3 см и R2=6 см. Пространство между сферами заполнено парафином (=2,0). Заряд Q1 внутренней сферы равен –1 нКл, внешний Q2=2 нКл. Найти потенциал φ электрического поля на расстоянии: 1) r1=1 см; 2) r2=5 см; от центра сфер. 1/(4π0)=9·109 м/Ф.
1) [75] 2) [135]
2. Металлический шар радиусом R=5 см несет заряд Q=1 нКл. Шар окружен слоем эбонита (=3,0) толщиной d=2 см. Вычислить потенциал φ электрического поля на расстоянии: 1) r1=3 см; 2) r2=6 см от центра шара. Построить график зависимости φ(r). 1/(4π0)=9·109 м/Ф. Полученный ответ округлите до целого значения.
1) [146] [145] 2) [136] [135]
3. Две круглые металлические пластины радиусом R=10 см каждая, заряженные разноименно, расположены одна против другой параллельно друг другу и притягиваются с силой F=2 мН. Расстояние d между пластинами 1 см. Определить разность потенциалов между пластинами. 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения. [1200] [1199]
Уровень 5 (Интегрирование).
1. Тонкая круглая пластина несет равномерно распределенный по плоскости заряд Q=1 нКл. Радиус R пластины равен 5 см. Определить потенциал φ электрического поля в двух точках: 1) в центре пластины; 2) в точке, лежащей на оси, перпендикулярной плоскости пластины и отстоящей от центра пластины на а=5 см. 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения.
1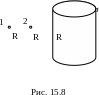
)
[360] [359] 2) [149] [150]
2. Электрическое поле создано бесконечно длинным равномерно заряженным (σ=0,1 мкКл/м2) цилиндром радиусом R=5 см. Определить изменение ΔП потенциальной энергии однозарядного положительного иона при перемещении его из точки 1 в точку 2 (рис. 15.8). Ответ запишите в электронвольтах. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [229] [230]
03.04. Потенциал поля зарядов, распределенных по объему (Потенциал объемного заряда)
Уровень 2.
1. Эбонитовый (=3,0) толстостенный полый шар несет равномерно распределенный по объему заряд с плотностью ρ=2 мкКл/м3. Внутренний радиус R1 шара равен 3 см, наружный R2=6 см. Определить потенциал φ шара на наружной поверхности шара. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [237] [238]
Уровень 5 (Интегрирование).
1. Плоская стеклянная (=7,0) пластинка толщиной d=2 см заряжена равномерно с объемной плотностью ρ=10 мкКл/м3. Найти разность потенциалов Δφ между точкой, лежащей на поверхности пластины, и точкой, находящейся внутри пластины в ее середине. Считать, что размеры пластины велики по сравнению с ее толщиной. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [8] [9]
2. Сплошной парафиновый (=2,0) шар радиусом R=10 см равномерно заряжен с объемной плотностью ρ=1 мкКл/мЗ. Определить потенциал φ электрического поля в центре шара. Построить график зависимости φ(r). 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [471] [470]
03.05. Разность потенциалов. Градиент потенциала и его связь с напряженностью поля (Разность потенциалов)
Уровень 1.
1. Разность потенциалов между двумя точками, находящимися на расстоянии 0,03 м друг от друга и лежащими на одной силовой линии однородного электрического поля, равна 12 В. Найдите разность потенциалов между точками, лежащими на той же силовой линии на расстоянии 15 см друг от друга. [60]
2. Напряженность электрического поля в плоском конденсаторе 30 кВ/м. Разность потенциалов между обкладками 300 В. Каково расстояние (в мм) между обкладками конденсатора? [10]
3. Две параллельные металлические пластины, находящиеся на расстоянии 0,1 м друг от друга в вакууме, заряжены до разности потенциалов 1 кВ. Какая сила будет действовать на заряд 10–4 Кл, помещенный между пластинами? Поле между пластинами считать однородным. [1]
4. В двух вершинах равностороннего треугольника со стороной 30 см находятся заряды 50 нКл каждый. Найдите потенциал (в кВ) в третьей вершине. k=9·109 м/Ф. [3]
5. В трех вершинах правильного тетраэдра с ребром 30 см находятся точечные заряды 3, 5 и –2 нКл. Найдите потенциал в четвертой вершине, k=9·109 м/Ф. [180]
6. В трех вершинах правильного шестиугольника со стороной 27 см находятся заряды 1 нКл, а в трех других – заряды 2 нКл. Найдите потенциал в центре шестиугольника, k=9·109 м/Ф. [300]
7. В центре сферы, несущей равномерно распределенный положительный заряд 10 нКл, находится маленький шарик с отрицательным зарядом –5 нКл. Найдите потенциал электрического поля в точке, находящейся вне сферы на расстоянии 9 м от ее центра, k=9·109 м/Ф. [5]
8. Бесконечная плоскость равномерно заряжена с поверхностной плотностью σ=4 нКл/м2. Определить значение и направление градиента потенциала электрического поля, созданного этой плоскостью. 0=8,85·10–12 Ф/м. Полученный ответ округлите до целого значения. [226] [225]
9. Напряженность Е однородного электрического поля равна 12000 В/м. Определить разность потенциалов U между этой точкой и другой, лежащей на той же силовой линии и отстоящей от первой на Δr=1 мм. [12]
10. Бесконечная тонкая прямая нить несет равномерно распределенный по длине нити заряд с плотностью τ=1 нКл/м. Каков градиент потенциала в точке, удаленной на расстояние r=10 см от нити? Указать направление градиента потенциала. 1/(2π0)=18·109 м/Ф. [180]
Уровень 2.
1. Между горизонтальными пластинами плоского конденсатора находится в равновесии пылинка массой 4,8·10–12 кг. Во сколько раз заряд пылинки больше заряда электрона, если напряжение на конденсаторе 3000 В, а расстояние между пластинами 2 см? Заряд электрона 1,6·10–19 Кл, g=10 м/с2. [2000]
2. Между горизонтальными пластинами плоского конденсатора на пластмассовой пружине подвешен заряженный шарик. Когда конденсатор присоединяют к источнику напряжения с ЭДС 500 В, пружина растягивается на 1 см. Найдите заряд (в мкКл) шарика, если жесткость пружины 10 Н/м, а расстояние между пластинами конденсатора 20 см. [40]
3. Электрон через отверстие в обкладке влетает в поле плоского конденсатора в направлении линий напряженности и полностью теряет свою скорость, пройдя путь 0,003 м. На каком расстоянии (в мм) электрон потеряет скорость, если его начальную скорость и разность потенциалов конденсатора уменьшить в 3 раза? [1]
4. В вершинах равнобедренного прямоугольного треугольника находятся точечные заряды 1, 2 и 3 нКл. Чему равен потенциал в середине гипотенузы, если ее длина 20 см? k=9·109 м/Ф. [540]
5. По тонкому кольцу радиусом 6 см распределен заряд 4 нКл. Найдите потенциал поля кольца в точке, лежащей на оси кольца на расстоянии 8 см от его центра, k=9·109 м/Ф. [360]
6. Напряженность Е однородного электрического поля в некоторой точке равна 6000 В/м. Вычислить разность потенциалов U между этой точкой и другой, лежащей на прямой составляющей угол α=60° с направлением вектора напряженности. Расстояние, между точками равно 2 мм. [60]
7. Электрическое поле создано положительным точечным зарядом. Потенциал поля в точке, удаленной от заряда на r=12 см, равен 24 В. Определить значение и направление градиента потенциала в этой точке. [200]
Уровень 3.
1. Отрицательно заряженная пылинка массой 10–9 г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. К конденсатору приложена разность потенциалов 500 В. На сколько вольт надо изменить разность потенциалов между пластинами, чтобы пылинка осталась в равновесии после того, как с нее стекло 500 электронов? Расстояние между пластинами 5 мм. Заряд электрона 1,6·10–19 Кл, g=10 м/с2. [2000]
2. Заряженная частица движется против линий напряженности однородного электрического поля. Начальная скорость частицы 1 Мм/с, ее удельный заряд 1011 Кл/кг. Какое расстояние (в см) пройдет частица до остановки, если напряженность поля равна 100 В/м? [5]
Уровень 4.
1. В плоский конденсатор длиной 10 см и с расстоянием между обкладками 1 см влетает электрон с энергией 8·10–15 Дж под углом 15° к пластинам. Чему равно напряжение между пластинами, при котором электрон на выходе из конденсатора будет двигаться параллельно им? Заряд электрона 1,6·10–19 Кл. [2500]
2. Шарик массой 10 г, имеющий заряд 100 мкКл, подвешен на нити длиной 50 см. Он находится в однородном электрическом поле с напряженностью 100 В/м, силовые линии которого горизонтальны и направлены слева направо. Шарик отвели влево так, что он оказался на 30 см ниже точки подвеса нити, и отпустили. Найдите силу натяжения (в мН) нити в тот момент, когда она проходит вертикальное положение, g=10 м/с2. [196]
Уровень 5 (Интегрирование).
1.
Сплошной шар из диэлектрика (ε=3) радиусом
R=10
см
заряжен с объемной плотностью ρ=50
нКл/мЗ.
Напряженность электрического поля
внутри и на поверхности такого шара
выражается формулой
,
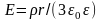здесь
r
–
расстояние от центра шара до точки, в
которой вычисляется напряженность
поля. Вычислить разность потенциалов
Δφ между центром шара и точками, лежащими
на его поверхности. 0=8,85·10–12
Ф/м. Полученный ответ умножьте на 100 и
округлите до целого значения. [314] [313]
03.06. Работа по перемещению зарядов в поле
Уровень 1.
1. Какую работу (в мкДж) совершает электростатическое поле при перемещении заряда 2 нКл из одной точки поля в другую, если разность потенциалов между ними равна 500 В? [1]
2. Какая работа совершается при переносе заряда 8 мкКл из точки поля с потенциалом 20 В в другую точку с потенциалом 12 В? В ответе укажите абсолютную величину работы в мкДж. [64]
3. Точечные заряды Q1=1 мкКл и Q2=0,1 мкКл находятся на расстоянии r1=10 см друг от друга. Какую работу А совершат силы поля, если второй заряд, отталкиваясь от первого, удалится от него на расстояние r3=∞. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 103. [9]
Уровень 2.
1. Точечные заряды Q1=1 мкКл и Q2=0,1 мкКл находятся на расстоянии r1=10 см друг от друга. Какую работу А совершат силы поля, если второй заряд, отталкиваясь от первого, удалится от него на расстояние r2=10 м. 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 105. [891]
2. Тонкий стержень согнут в полукольцо. стержень заряжен с линейной плотностью τ=133 нКл/м. Какую работу А надо совершить, чтобы перенести заряд Q=6,7 нКл из центра полукольца в бесконечность? 0=8,85·10–12 Ф/м. Полученный ответ умножьте на 106 и округлите до целого значения. [25] [26]
3
.
Определить работу А1,2
сил поля по перемещению заряда Q=1
мкКл из точки 1 в точку 2 поля,
созданного
заряженным проводящим шаром (рис. 15.15).
Потенциал φ шара равен 1 кВ. Полученный
ответ умножьте на 106.
[250]
Уровень 3.
1. При переносе точечного заряда 10 нКл из бесконечности в точку, находящуюся на расстоянии 20 см от поверхности равномерно заряженного шара, необходимо совершить работу 0,5 мкДж. Радиус шара 4 см. Найдите потенциал на поверхности шара. [300]
2. Работа электрического поля при перемещении отрицательно заряженной частицы по направлению к закрепленной частице, заряженной положительно, равна 9 Дж. При этом частица переместилась на половину первоначального расстояния до закрепленной частицы. Какая работа совершена электрическим полем на первой половине этого пути? [3]
3. Скорость заряженной частицы массой 2 г в начальной точке движения равна 0,02 м/с, а в конечной 0,1 м/с. Найдите разность потенциалов между этими точками, если заряд частицы равен 30 нКл. [320]
4. Возле поверхности шара радиусом 6 см, равномерно заряженного зарядом 4 нКл, находится частица массой 30 мг с зарядом 2 нКл. Частицу освобождают. Найдите скорость (в см/с) частицы в тот момент, когда она удалится от поверхности шара на расстояние, равное его радиусу, k=9·109 м/Ф. [20]
5. В трех вершинах равнобедренного прямоугольного треугольника закреплены одинаковые точечные заряды по 20 нКл каждый. Посередине гипотенузы помещают заряженную частицу массой 3 мг и зарядом 40 нКл и отпускают. Какую скорость приобретет частица на большом расстоянии от зарядов? Гипотенуза треугольника 5 см. k=9·109 м/Ф. [24]
6. В двух вершинах равностороннего треугольника со стороной 12 см закреплены точечные заряды по 6 нКл каждый, а в третьей вершине находится частица массой 6 мг, несущая заряд –30 нКл. Частицу отпускают, и она приходит в движение. Чему равна скорость частицы в тот момент, когда она находится точно между зарядами? k=9·109 м/Ф. [3]
7. По тонкому кольцу радиусом 4 см равномерно распределен заряд 50 нКл. На оси кольца на расстоянии 3 см от его центра помещают частицу с зарядом –18 нКл и массой 1 мг и отпускают. Найдите скорость частицы в тот момент, когда она будет пролетать через центр кольца. k=9·109 м/Ф. [9]
8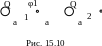
.
Электрическое поле создано двумя
одинаковыми положительными точечными
зарядами Q.
Найти работу А1,2
сил
поля по перемещению заряда Q1=10
нKл из точки 1 с потенциалом φ1=300
В в точку 2 (рис. 15.10). Полученный ответ
умножьте на 106.
[1]
9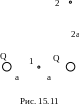
.
Определить работу А1,2
по перемещению заряда Q1=50
нКл из точки 1 в точку 2 (рис. 15.11) в поле,
созданном двумя точечными зарядами,
модуль |Q|
которых равен 1 мкКл и a=0,1
м.
1/(4π0)=9·109
м/Ф. Полученный ответ умножьте на 106
и округлите до целого значения. [659] [660]
1
0.
Электрическое поле создано бесконечной
равномерно заряженной плоскостью с
поверхностной плотностью заряда σ=2
мкКл/м2.
В этом поле вдоль прямой, составляющей
угол α=60˚ с плоскостью, из точки 1 в точку
2, расстояние ℓ
между
которыми равно 20 см (рис. 15.12), перемещается
точечный электрический заряд Q=10
нКл.
Определить работу А
сил
поля по
перемещению
заряда. 0=8,85·10–12
Ф/м. Полученный ответ умножьте на 100 и
округлите до целого значения. [196] [195]
1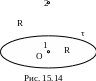
1.
Тонкий стержень согнут в кольцо радиусом
R=10
см.
Он заряжен с линейной плотностью τ=300
нКл/м. Какую работу А
надо
совершить, чтобы перенести заряд Q=5
нКл
из центра кольца в точку, расположенную
на оси кольца на расстоянии ℓ=20
см от центра его? 0=8,85·10–12
Ф/м. Полученный ответ умножьте на 106
и округлите до целого значения. [47] [46]
12. Электрическое поле создано равномерно распределенным по кольцу зарядом (τ=1 мкКл/м). Определить работу А1,2 сил поля по перемещению заряда Q=10 нКл из точки 1 (в центре кольца) в точку 2, находящуюся на перпендикуляре к плоскости кольца (рис.15.14). 0=8,85·10–12 Ф/м. Полученный ответ умножьте на 106 и округлите до целого значения. [165] [166]
Уровень 5 (Интегрирование).
1
.
На отрезке прямого провода равномерно
распределен заряд с линейной плотностью
τ=1
мкКл/м. Определить работу А
cил
поля по перемещению заряда Q=1
нКЛ из точки В
в точку С
(рис. 15.13). 0=8,85·10–12
Ф/м. Полученный ответ умножьте на 108
и округлите до целого значения. [259] [258]
2. Бесконечная прямая нить несет равномерно распределенный заряд (τ=0,1 мкКл/м). Определить работу A1,2 сил поля по перемещению заряда Q=50 нКл из точки 1 в точку 2 (рис. 15.16). 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ умножьте на 106 и округлите до целого значения. [62] [63]
03.07. Движение заряженных частиц в электрическом поле (Движение заряда в эл. поле)
Уровень 1.
1. Пылинка массой т=1 пг, несущая на себе пять электронов, прошла в вакууме ускоряющую разность потенциалов U=3 МВ. Какова кинетическая энергия Т пылинки? Заряд электрона e=1,6·10–19 Кл. Полученный ответ умножьте на 1013. [24]
Уровень 2.
1. Заряженная частица, пройдя ускоряющую разность потенциалов U=600 кВ, приобрела скорость υ=5,4 Мм/с. Определить удельный заряд частицы (отношение заряда к массе). Полученный ответ умножьте на 10–5. [243]
Уровень 3.
1. Электрон находится в однородном электрическом поле напряженностью Е=200 кВ/м. 1) Какой путь пройдет электрон за время t=1 нс, если его начальная скорость была равна нулю? 2) Какой скоростью будет обладать электрон в конце этого интервала времени? Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ умножьте на 1) 103 2) 10–6 и округлите до целого значения.
1) [18] [17] 2) [35] [36]
2. Какая ускоряющая разность потенциалов U требуется для того, чтобы сообщить скорость υ=30 Мм/с: 1) электрону; 2) протону (полученный ответ умножьте 10–3). Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг, масса протона m=1,67·10–27 кг. Полученный ответ округлите до целого значения.
1) [2559] [2560] 2) [4697] [4696]
3. Разность потенциалов U между катодом и анодом электронной лампы равна 90 В, расстояние r=1 мм. 1) Какова скорость υ электрона в момент удара об анод (полученный ответ умножьте 10–4)? 2) За какое время t электрон пролетает расстояние от катода до анода (полученный ответ умножьте 1012)? Поле считать однородным. Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ округлите до целого значения.
1) [563] [562] 2) [356] [357]
4. Пылинка массой т=1 пг, несущая на себе пять электронов, прошла в вакууме ускоряющую разность потенциалов U=3 МВ. Какую скорость υ приобрела пылинка? Заряд электрона e=1,6·10–19 Кл. Полученный ответ округлите до целого значения. [69] [70]
5. Протон, начальная скорость υ которого равна 100 км/с, влетел в однородное электрическое поле (Е=300 В/см) так, что вектор скорости совпал с направлением линий напряженности. Какой путь ℓ должен пройти протон в направлении линий поля, чтобы его скорость удвоилась? Заряд протона e=1,6·10–19 Кл, масса протона m=1,67·10–27 кг. Полученный ответ умножьте на 105 и округлите до целого значения. [522] [521]
6. Бесконечная плоскость заряжена отрицательно с поверхностной плотностью σ=35,4 нKл/м2. По направлению силовой линии поля, созданного плоскостью, летит электрон. Определить минимальное расстояние ℓmin, на которое может подойти к плоскости электрон, если на расстоянии ℓ0=5 см он имел кинетическую энергию Т=80 эВ. 0=8,85·10–12 Ф/м. Полученный ответ умножьте на 100. [1]
7. Электрон, летевший горизонтально со скоростью υ=1,6 Мм/с, влетел в однородное электрическое поле с напряженностью Е=90 В/см, направленное вертикально вверх. Какова будет 1) по модулю и 2) направлению (в ответе укажите угол между направлениями начальным и конечным) скорость υ электрона через 1 нс? Заряд электрона e=1,6·10–19 Кл, масса электрона m=9·10–31 кг. 1) Полученный ответ умножьте на 10–4 и округлите до целого значения.
1) [224] [223] 2) [45]
8. Вдоль силовой линии однородного электрического поля движется протон. В точке поля с потенциалом φ1=500 В протон имел скорость υ1=0,1 Мм/с. Определить потенциал φ2 точки поля, в которой скорость протона возрастает в n=2 раза. Отношение заряда протона к его массе е/m=96 МКл/кг. Полученный ответ округлите до целого значения. [344] [343]
9. В однородное электрическое поле напряженностью Е=1 кB/M влетает вдоль силовой линии электрон со скоростью υ0=1 Mм/c. определить расстояние ℓ; пройденное электроном до точки, в которой его скорость υ1 будет равна половине начальной. Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ умножьте на 105 и округлите до целого значения. [213] [214]
1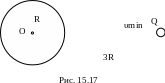
0.
Какой минимальной скоростью υmin
должен обладать протон, чтобы он мог
достигнуть поверхности заряженного до
потенциала φ=400 В металлического шара
(рис. 15.17)? Заряд протона e=1,6·10–19
Кл, масса протона m=1,67·10–27
кг. Полученный ответ умножьте на 10–3
и округлите до целого значения. [240] [239]
11. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом φ1=100 В электрон имел скорость υ1=6 Mм/c. Определить потенциал φ2 точки поля, в которой скорость υ2 электрона будет равна 0,5υ1. Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ умножьте на 10–3 и округлите до целого значения. [23] [24]
12. Электрон с начальной скоростью υ0=3 Мм/с влетел в однородное электрическое поле напряженностью Е=150 B/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Найти скорость υ электрона через t=0,1 мкс. Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ умножьте на 10–4 и округлите до целого значения. [400] [399]
13. Положительно заряженная частица, заряд которой равен элементарному заряду е, прошла ускоряющую разность потенциалов U=60 кВ и летит на ядро атома лития, заряд которого равен трем элементарным зарядам. На какое наименьшее расстояние rmin частица может приблизиться к ядру? Начальное расстояние частицы от ядра можно считать практически бесконечно большим, а массу частицы – пренебрежимо малой по сравнению с массой ядра. Заряд электрона e=1,6·10–19 Кл, 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 1015. [72]
14. Два электрона, находящиеся на большом расстоянии, друг от друга, сближаются с относительной начальной скоростью υ=10 Mм/c. Определить минимальное расстояние rmin на которое они могут подойти друг к другу. Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг, 1/(4π0)=9·109 м/Ф. Полученный ответ умножьте на 1012 и округлите до целого значения. [10] [11]
Уровень 4.
1. Электрон влетел в пространство между пластинами плоского конденсатора со скоростью υ=10 Mм/c, направленной параллельно пластинам. На сколько приблизится электрон к положительно заряженной пластине за время движения внутри конденсатора (поле считать однородным), если расстояние d между пластинами равно 16 мм, разность потенциалов U=30 В и длина ℓ пластин равна 6 см? Заряд электрона e=1,6·10–19 Кл, масса электрона m=9·10–31 кг. Полученный ответ умножьте на 103. [6]
2. Электрон влетел в плоский конденсатор, имея скорость υ=10 Mм/c, направленную параллельно пластинам. В момент вылета из конденсатора направление скорости электрона составляло угол α=35˚ с первоначальным направлением скорости. Определить разность потенциалов U между пластинами (поле считать однородным), если длина ℓ пластин равна 10 см и расстояние d между ними равно 2 см. Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ округлите до целого значения. [80] [79]
3. Электрон влетел в плоский конденсатор, находясь на одинаковом расстоянии от каждой пластины и имея скорость υ=10 Мм/с, направленную параллельно пластинам, расстояние d между которыми равно 2 см. Длина ℓ каждой пластины равна 10 см. Какую наименьшую разность потенциалов U нужно приложить к пластинам, чтобы электрон не вылетел из конденсатора? Заряд электрона e=1,6·10–19 Кл, масса электрона m=9,1·10–31 кг. Полученный ответ округлите до целого значения. [23] [22]
4
.
Протон сближается с альфа-частицей.
Скорость υ1
протона в лабораторной системе отсчета
на достаточно большом удалении от
альфа-частицы равна 300 км/с, а скорость
υ2
альфа-частицы
можно принять равной нулю. Определить
минимальное расстояние rmin,
на которое подойдет протон к альфа-частице.
Заряд альфа-чacтицы равен двум элементарным
положительным зарядам, а массу т1
ее
можно считать в четыре раза большей,
чем масса т2
протона.
Заряд протона e=1,6·10–19
Кл, масса протона m=1,67·10–27
кг. 1/(4π0)=9·109
м/Ф. Полученный ответ умножьте на 1014
и округлите до целого значения. [766] [767]
Уровень 5 (Интегрирование).
1. Из точки 1 на поверхности бесконечно длинного отрицательно заряженного цилиндра (τ=20 нKл/м) вылетает электрон (υ0=0). Определить кинетическую энергию Т электрона в точке 2, находящейся на расстоянии 9R от поверхности цилиндра, здесь R – его радиус (рис. 15.18). Ответ запишите в электронвольтах. Заряд электрона e=1,6·10–19 Кл, 0=8,85·10–12 Ф/м, π=3,14. Полученный ответ округлите до целого значения. [829] [828]