
Гармонические колебания формулы.
Дифференциальное уравнение гармонических колебаний:
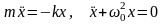 ;
;
здесь m – масса точки, k – коэффициент квазиупругой силы (k=mω02);
Уравнение механических гармонических колебаний:
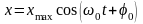 ,
,
здесь x – смещение от положения равновесия или значение колеблющейся величины, xmax – амплитуда колебаний, ω0 – циклическая собственная частота, t – время, φ0 – начальная фаза, (ω0t + φ0) – фаза колебаний;
Период колебаний:
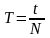 ,
,
здесь N – число колебаний за время t;
Частота колебаний:
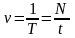 ;
;
Циклическая частота:
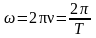 ,
,
Скорость и ускорение гармонических колебаний, соответственно:
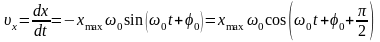 ,
,
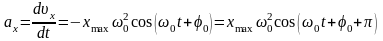 ;
;
Собственная частота и период колебаний математического маятника:
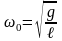 ,
,
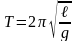 ,
,
здесь g – ускорение свободного падения, ℓ – длина подвеса;
Собственная частота и период колебаний физического маятника:
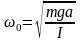 ,
,
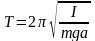 ,
,
здесь I – момент инерции физического маятника относительно оси колебаний, a – расстояние от центра масс маятника до оси колебаний;
Собственная частота и период колебаний пружинного маятника:
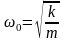 ,
,
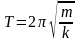 ,
,
здесь k – жёсткость пружины, m – масса тела, прикреплённого к пружине;
Период крутильных колебаний на упругой нити:
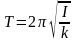 ,
,
здесь I – момент инерции тела относительно оси, совпадающей с упругой нитью, k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается;
Сила, возвращающая тело в положение равновесия в пружинном маятнике:
Fвозвр=kx,
здесь k=mω02;
Кинетическая энергия, потенциальная энергия, полная энергия пружинного маятника, соответственно:
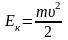 ,
,
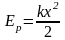 ,
,
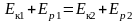 ;
;
Амплитуда A результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле:
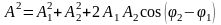 ;
;
здесь A1, A2 – амплитуды составляющих колебаний, φ1, φ 2 – их начальные фазы;
Начальная фаза φ результирующего колебания может быть найдена из формулы
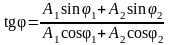 ;
;
Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν1, ν2:
ν=ν1 – ν2;
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты с амплитудами A1 и A2 начальными фазами φ1 и φ2:
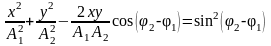 ;
;
Если начальные фазы φ1 и φ2 составляющих колебаний одинаковы, то уравнение траектории принимает вид:
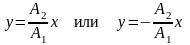 ,
,
т. е. точка движется по прямой;
В том случае, если разность фаз Δφ=φ 2 – φ1=π/2, принимает вид
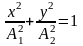 ,
,
т. е. точка движется по эллипсу;
Дифференциальное уравнение затухающих колебаний:
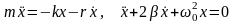 ,
,
здесь m – масса точки, r – коэффициент сопротивления, β – коэффициент затухания, β=r/(2m);
Уравнение механических затухающих колебаний:
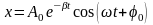 ,
,
здесь
A0
– начальная амплитуда,
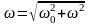 – частота затухающих колебаний;
– частота затухающих колебаний;
Время релаксации, логарифмический декремент затухания и добротность, соответственно:
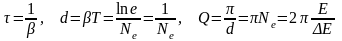 ,
,
здесь Ne – число колебаний, в течении которых амплитуда колебаний уменьшается в «e», E – среднее значение запасенной энергии в системе за некоторый промежуток времени, равный одному периоду колебаний, ΔE –потери энергии системе за тот же промежуток времени;
Дифференциальное уравнение вынужденных колебаний:
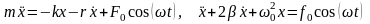 ,
,
здесь F0cos(ωt) – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания, F0 – ее амплитудное значение, F0=F0/m;
Амплитуда вынужденных колебаний:
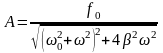 ,
,
Резонансная частота и резонансная амплитуда, соответственно:
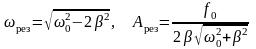 .
.
