
- •Физика сборник задач по механике
- •Введение
- •Количественное распределение задач по параграфам и по уровню сложности
- •01.01. Кинематика поступательного и вращательного движения формулы
- •01.01.01. Относительность движения. Сложение скоростей. Средняя скорость.
- •01.01.02. Равноускоренное движение. Движение в поле тяжести
- •01.01.03. Движение двух тел. Несколько последовательных этапов движения
- •01.01.04. Горизонтальный бросок. Бросок под углом
- •01.01.05. Вращательное движение. Криволинейное движение
- •01.02. Динамика поступательного движения формулы
- •01.02.01. Второй закон Ньютона
- •01.02.02. Коэффициент трения. Наклонная плоскость с трением
- •01.02.03. Динамика материальной точки, движущейся по окружности
- •01.03. Закон сохранения импульса тела. Столкновения частиц формулы
- •01.03.01. Импульс
- •01.03.02. Закон сохранения импульса
- •01.04. Закон сохранения энергии формулы
- •01.04.01. Работа и энергия
- •01.04.02. Мощность (постоянная, переменная, средняя)
- •01.04.03. Кинетическая энергия. Потенциальная энергия
- •01.04.04. Закон сохранения энергии
- •01.04.05. Закон сохранения энергии. Закон сохранения импульса. Упругий, неупругий удары
- •01.05. Динамика вращательного движения формулы
- •01.05.01. Момент инерции
- •01.03.02. Основное уравнение динамики вращательного движения
- •01.05.03. Закон сохранения момента импульса
- •01.05.04. Работа и энергия
- •01.05.05. Центр масс
- •01.06. Силы в механике формулы
- •01.06.01. Силы тяготения. Гравитационное поле. Спутники
- •01.06.02. Силы упругости. Механическое напряжение
- •01.06.03. Работа упругой силы. Энергия деформированного тела
- •01.07. Релятивистская механика формулы
- •01.07.01. Релятивистское изменение длин и интервалов времени
- •01.07.02. Релятивистское сложение скоростей
- •01.07. 03. Релятивистская масса и релятивистский импульс
- •01.07.04. Взаимосвязь массы и энергии
- •01.07.05. Кинетическая энергия релятивистской частицы
- •01.07.06. Связь энергии релятивистской частицы с ее импульсом
- •01.08. Механические колебания формулы
- •01.08.01. Кинематика гармонических колебаний
- •01.08.02. Сложение колебаний
- •01.08.03. Динамика гармонических колебаний. Маятники
- •01.08.04. Затухающие колебания
- •01.08.05. Вынужденные колебания. Резонанс
- •01.09. Волны в упругой среде. Акустика формулы
- •01.09.01. Уравнение плоской волны
- •01.09.02. Скорость звука
- •01.09.03. Суперпозиция волн
- •01.09.04. Эффект Доплера
- •01.07.05. Энергия звуковых волн
- •Список используемой литературы
01.01. Кинематика поступательного и вращательного движения формулы
Положение материальной точки в пространстве:
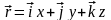 ,
,
здесь
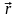 – радиус-вектор,
– радиус-вектор,
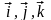 – единичные векторы направлений (орты),
x,
y,
z
– координаты точки.
– единичные векторы направлений (орты),
x,
y,
z
– координаты точки.
Средняя и мгновенная скорости, соответственно:
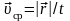 ,
,
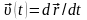 ,
,
здесь
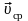 – средняя скорость, t
– время,
– средняя скорость, t
– время,
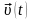 – мгновенная скорость в момент времени
t,
– мгновенная скорость в момент времени
t,
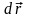 – изменение (приращение) положения
(дифференциал перемещения), dt
– промежуток времени (дифференциал
времени),
– изменение (приращение) положения
(дифференциал перемещения), dt
– промежуток времени (дифференциал
времени),
 – производная перемещения.
– производная перемещения.
Средняя и мгновенная путевые скорости:
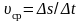 ,
,
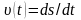 ,
,
здесь
Δs
– путь, пройденный телом за интервал
времени Δt,
ds
– изменение (приращение) пути (дифференциал
пути), dt
– промежуток времени (дифференциал
времени),
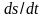 – производная пути.
– производная пути.
Относительность движения (закон сложения скоростей):
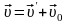 ,
,
здесь
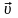 – скорость тела относительно неподвижной
системы отсчёта,
– скорость тела относительно неподвижной
системы отсчёта,
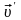 – скорость тела относительно подвижной
системы отсчёта,
– скорость тела относительно подвижной
системы отсчёта,
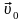 – скорость подвижной системы отсчёта.
– скорость подвижной системы отсчёта.
Произвольное движение.
Модуль перемещения:
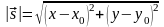 ,
,
здесь
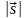 – модуль перемещения, x,
y
– конечные координаты, x0,
y0
– начальные координаты;
– модуль перемещения, x,
y
– конечные координаты, x0,
y0
– начальные координаты;
Мгновенное ускорение:
 ,
,
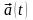 – мгновенное
ускорение;
– мгновенное
ускорение;
Тангенциальное и нормальное (центростремительное) ускорения, соответственно:
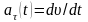 ,
,
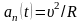 ,
,
здесь aτ – тангенциальное ускорение, an – нормальное ускорение;
Полное ускорение или сумма тангенциального и нормального ускорений:
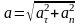 .
.
Движение
с постоянным по величине и направлению
ускорением
(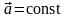 ),
разложение движения по направлениям
(зависимость координат x
и y
и проекций скорости υx
и υy
от времени, соответственно):
),
разложение движения по направлениям
(зависимость координат x
и y
и проекций скорости υx
и υy
от времени, соответственно):

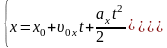 ;
;
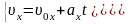 ,
,
здесь x0, y0 – начальные координаты, υ0 – начальная скорость, υ0x, υ0y – проекции начальной скорости на оси X и Y;
Полная скорость:
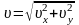 ;
;
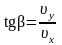 ,
,
здесь β – угол между вектором скорости υ и проекцией вектора скорости υx на ось X;
Если
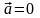 ,
,
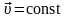 (равномерное
движение вдоль прямой линии):
(равномерное
движение вдоль прямой линии):
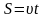 ;
;
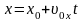 .
.
Если
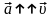 или
или
 (равноускоренное или равнозамедленное
движение вдоль прямой линии):
(равноускоренное или равнозамедленное
движение вдоль прямой линии):
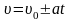 ;
;
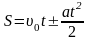 ;
;
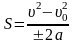 ;
;
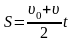 ;
;
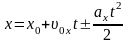 .
.
Если
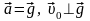 (горизонтальный бросок в поле тяжести
Земли, движение тела по параболе):
(горизонтальный бросок в поле тяжести
Земли, движение тела по параболе):
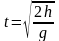 ;
;
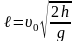 ;
;
 ,
,
здесь t – время падения (или время полёта), g – ускорение свободно падения, h – высота начального положения тела над поверхностью Земли, ℓ – дальность броска (полёта), υ1 – скорость тела в момент времени t1.
Если
 и
– угол между
и
– угол между
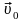 и
и
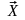 (бросок под углом к горизонту, движение
тела по параболе):
(бросок под углом к горизонту, движение
тела по параболе):
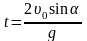 ;
;
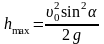 ;
;
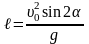 ,
,
здесь t – время полёта, hmax – максимальная высота полёта, ℓ – дальность полёта.
Равномерное движение по окружности:
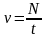 ;
;
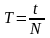 ;
;
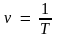 ;
;
 ;
;
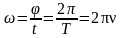 ;
S
= φR;
;
S
= φR;
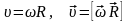 ;
;
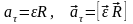 ;
;

здесь ν – частота (количество оборотов за 1 секунду), N – количество оборотов, t – время вращения, T – период обращения (время одного полного оборота), υ – скорость движения по окружности, R – радиус окружности, ω – циклическая частота или угловая скорость вращения, φ – угол поворота, aτ – тангенциальное ускорение; aцс (an) – центростремительное ускорение или нормальное ускорение, ε – угловое ускорение.
Кинематическое уравнение равномерного вращения (ω = const):
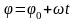 ,
,
Кинематическое уравнение равнопеременного вращения (ε = const):
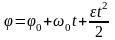 ,
,
здесь φ0 – начальное угловое перемещение, ω0 – начальная угловая скорость.
ЗАДАЧИ
