1.05. Динамика вращательного движения формулы

Равномерное движение по окружности:

; ; ;

; ; S = φR;

;

_;

здесь ν – частота (количество оборотов за 1 секунду), N – количество оборотов, t – время вращения, T – период обращения (время одного полного оборота), υ – скорость движения по окружности, R – радиус окружности, ω – циклическая частота или угловая скорость вращения, φ – угол поворота, a_τ – тангенциальное ускорение; a_цс (a_n) – центростремительное ускорение или нормальное ускорение, ε – угловое ускорение.

Кинематическое уравнение равномерного вращения (ω = const):

,

Кинематическое уравнение равнопеременного вращения (ε = const):

,

здесь φ₀ – начальное угловое перемещение, ω₀ – начальная угловая скорость.

Момент инерции относительно оси вращения материальной точки:

,

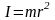здесь m – масса материальной точки, r – расстояние от оси вращения до материальной точки;

Момент инерции относительно оси вращения системы материальных точек:

,

здесь m_i – масса i-й элементарной точки, r_i – расстояние от материальной точки до оси вращения;

Момент инерции относительно оси вращения твердого тела:

,

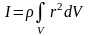здесь ρ – плотность тела;

Момент инерции некоторых тел правильной геометрической формы:

Однородный тонкий стержень массой m и длиной ℓ, ось проходит перпендикулярно стержню через центр стержня, через его край, соответственно:

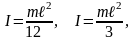
Тонкое кольцо, обруч, труба массой m и радиусом R, ось проходит перпендикулярно плоскости тела через центр:

,

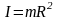Круглый однородный диск массой m и радиусом R, ось проходит перпендикулярно плоскости диска через центр:

,

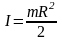Однородный шар массой m и радиусом R, ось проходит через центр шара:

,

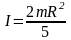Однородная сфера массой m и радиусом R, ось проходит через центр сферы:

;

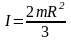Для плоских фигур:

,

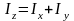здесь Iz – момент инерции плоской фигуры относительно оси Oz, перпендикулярной плоскости; Ix и Iy – момент инерции той же фигуры относительно осей Ox и Oy, лежащих в плоскости;

Теорема Штейнера:

,

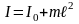здесь I – момент инерции тела относительно произвольной оси, I₀ – момент инерции тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси, ℓ – расстояние между осями, m – масса тела;

Момент силы F, действующей на тело, относительно оси вращения:

,

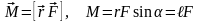здесь r – радиус-вектор, направленный от оси вращения к точке приложения силы F, ℓ – плечо силы (кратчайшее расстояние от оси вращения до линии действия силы, α – угол между радиус-вектором и силой;

Момент импульса вращающегося тела относительно оси:

;

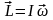Закон сохранения момента импульса

;

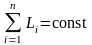Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:

;

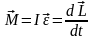Работа момента силы, действующего на вращающееся тело:

,

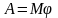здесь φ – угол поворота тела;

Кинетическая энергия вращающегося тела:

,

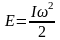Кинетическая энергия тела, катящегося по плоскости:

.

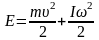Примеры решения задач

1. К концу нити, намотанной на блок с моментом инерции I = 0,08 кг·м² и радиусом R = 0,1 м, привязали тело массой m = 2 кг и отпустили. Найти угловое ускорение тела.

Дано: I = 0,08 кг·м2; R = 0,1 м; m = 2 кг; g = 9,8 м/с2;	Решение: Запишем второй закон Ньютона для тела: и основное уравнение динамики вращательного движения для блока (T – сила натяжения нити) .
a – ?

С учетом соотношения

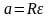
получим выражение для вычисления ускорения a:

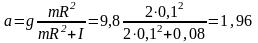м/с².

Ответ: a = 1,96 м/с².

2. Вычислите момент инерции шара массой 0,2 кг и радиусом 0,05 м относительно оси, которая проходит на расстоянии 0.1 м от центра шара.

Дано: ℓ = 0,1·м; R = 0,05 м; m = 0,2 кг;	Решение: Момент инерции однородного шара, относительно оси, которая проходит через центр масс шара .
I – ?

Момент инерции относительно оси, не проходящей через центр масс, вычислим с помощью теоремы Штейнера

.

Таим образом, момент инерции шара равен

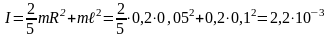кг·м².

Ответ: I = 2,2·10^-3 кг·м².

3. Физический маятник представляет собой стержень длиной ℓ = 1 м и массой m₁ = 1 кг с прикрепленным к одному из его концов шаром массой m₂ = 0,5 кг и радиусом R = 0,2 м. Определить момент инерции такого маятника относительно оси, проходящей через другой конец стержня и перпендикулярной стержню.

Дано: m1 = 1 кг; m2 = 0,5 кг; ℓ = 1 м/с;	Решение: Момент инерции для стержня и шара, относительно оси, проходящей через центр масс, соответственно
I – ?

_{М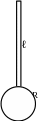 омент инерции относительно заданной оси найдем по теореме Штейнера (см. рис.)}

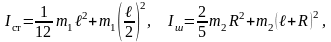
Момент инерции всей системы равен

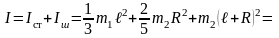
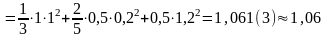кг∙м².

Ответ: I = 1,06 кг∙м².

4. Маховик в виде диска массой m = 50 кг и радиусом r = 20 см был раскручен до частоты вращения n₁ = 480 мин^-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент M сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t = 50 с; 2) маховик до полной остановки сделал N = 200 оборотов.

Дано: m = 50 кг; r = 0,2 м; n1 = 8 с-1; t = 50 с; N = 200 об;	Решение: 1) По основному закону динамки вращательного движения изменение момента импульса вращающегося тела равно произведению момента сил, действующего на тело, на время действия этой силы , здесь I – момент инерции маховика, ω1 и ω2 – начальная и конечная угловые скорости.
M – ?

В нашем случае ω₂ = 0, Δt = t → Mt = –Iω₁, откуда

,

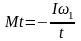Момент инерции диска относительно его геометрической оси равен I = mr²/2. Подставив это выражение в основной закон динамики вращательного движения, получаем

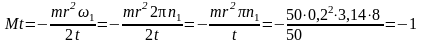Н∙м.

2) Запишем закон сохранения энергии, согласно которому в данной задаче вся кинетическая энергия вращения маховика была потрачена на работу сил трения

,

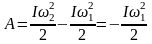с учетом того, что ω₂ = 0.

Работа момента силы равна A = Mφ. Подставляя это выражение в закон сохранения энергии, получим

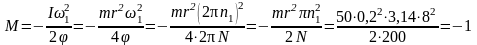Н∙м.

Ответ: M = – 1 Н∙м.

5. Платформа в виде диска радиусом R = 1,5 м и массой m₁ = 180 кг вращается по инерции около вертикальной оси с частотой n₁ = 10 мин^-1. В центре платформы стоит человек массой m₂ = 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Дано: m1 = 180 кг; m2 = 60 кг; R = 1,5 м; n1 = 10 мин-1;	Решение: По закону сохранения момента импульса , здесь I1 – момент инерции платформы, I2 – момент инерции человека, стоящего в центре платформы, ω – угловая скорость платформы с человеком, стоящим в ее центре, I՛2 – момент инерции человека, стоящего на краю платформы, ω՛ – угловая скорость платформы с человеком, стоящим на ее краю.
υ – ?

_{Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением}

_υ = ω՛R.

Объединив оба уравнения, получим следующее выражение

.

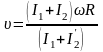_{Момент инерции платформы рассчитываем, как для диска, следовательно,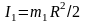} . Момент инерции человека рассчитываем, как для материальной точки. Поэтому 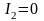, 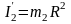. Угловая скорость платформы до перехода человека равна ω = 2πn.

_{Используя эти выражения, перепишем формулу для скорости}

.

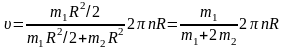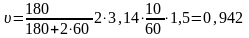м/с.

Ответ: υ = 0,942 м/с.
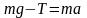
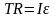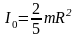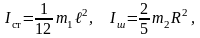
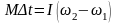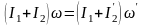