
- •1.01. Кинематика поступательного и вращательного движения формулы
- •Примеры решения задач
- •1.02. Динамика поступательного движения формулы
- •Примеры решения задач
- •1.03. Закон сохранения импульса тела. Столкновения частиц формулы
- •Примеры решения задач
- •1.04. Закон сохранения энергии формулы
- •Примеры решения задач
- •1.05. Динамика вращательного движения формулы
- •Примеры решения задач
- •1.06. Гармонические колебания формулы
- •Дополнительно. Волны в упругой среде. Акустика
- •Примеры решения задач
- •1.07. Уравнение состояния идеального газа. Молекулярно-кинетическая теория формулы
- •Примеры решения задач
- •1.08. Первое начало термодинамики формулы
- •Примеры решения задач
- •Список используемой литературы
- •Введение
- •Рекомендации по решению задач
- •Требования к оформлению
- •Критерии и шкала оценивания устной защиты решения задач
1.04. Закон сохранения энергии формулы
Работа силы F:
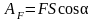 ,
,
здесь S – перемещение, α – угол между вектором силы F и вектором перемещения S;
Мощность:
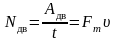 ,
,
здесь Nдв – мощность двигателя, Aдв – работа двигателя, совершённая за время t, Fт – сила тяги двигателя, υ – скорость движения;
Кинетическая энергия:
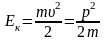 ,
,
здесь m – масса тела, υ – скорость тела, p – импульс тела;
Потенциальная энергия относительно поверхности Земли:
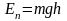 ,
,
здесь m – масса тела, g – ускорение свободного падения, h – высота тела над поверхностью Земли;
Работа и изменение энергии:
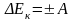 ,
,
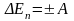 ;
;
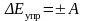 ,
,
здесь ΔEк – изменение кинетической энергии в результате совершения над телом работы A, ΔEп – изменение потенциальной энергии в результате совершения над телом работы A, ΔEупр – изменение потенциальной энергии упругой деформации в результате совершения над телом работы A;
Закон сохранения механической энергии:
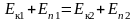 ,
,
здесь Eк1,2 – суммарная кинетическая энергия системы, Eп1,2 – суммарная потенциальной энергия системы;
Коэффициент полезного действия;
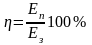 ,
,
здесь Eп – полезная энергия, выработанная энергетической машиной, Eз – затраченная энергия.
Относительная деформация при продольном растяжении или сжатии тела:
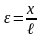 ,
,
здесь ℓ – начальная длина тела, x – величина растяжения или сжатия;
Относительная деформация при сдвиге определяется из формулы:
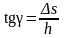 ,
,
здесь tgγ – относительный сдвиг, Δs – абсолютный сдвиг параллельных слоев тела относительно друг друга, h – расстояние между слоями, γ – угол сдвига;
Напряжение нормальное:
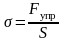 ,
,
здесь Fупр – упругая сила, перпендикулярная поперечному сечению тела, S – площадь этого сечения;
Напряжение тангенциальное:
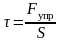 ,
,
здесь Fупр – упругая сила, действующая вдоль слоя тела, S – площадь этого сечения;
Закон Гука для продольного растяжения или сжатия:
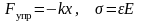 ,
,
здесь k – коэффициент упругости (жесткость пружины), E – модуль Юнга;
Закон Гука для сдвига:
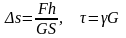 ,
,

здесь Δs – сдвиг верхнего края относительно основания, h –высота тела, G – модуль поперечной упругости (модуль сдвига);
Момент, закручивающий на угол φ однородный круглый стержень:
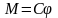 ,
,
здесь C – постоянная кручения;
Потенциальная энергия деформированной пружины (стержня):
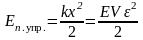 ,
,
здесь k – жесткость пружины, x – величина растяжения или сжатия пружины, E – модуль Юнга, V – объем стержня.
Примеры решения задач
1. Человек массой 60 кг спускается по лестнице длиной 15 м, расположенной под углом 30º к горизонтальной плоскости. Найдите работу силы тяжести.
Дано: m = 60 кг; s = 15 м/с; α = 30º; g = 9,8 м/с2; |
Решение: Работа
силы тяжести равна произведению модуля
вектора силы
на модуль вектора перемещения
Угол α нужно брать 30º, поэтому работа равна
|
A – ? |
Ответ: A = 4410 Дж.
2. Вычислите работу силы упругости при изменении деформации пружины жесткостью 300 Н/м от xl = 4 см до x2 = 8 см.
Дано: k = 300 Н/м; x1 = 4 м/с; x2 = 8 м/с; |
Решение: По закону Гука проекция вектора силы упругости ось ОХ, направленную по вектору перемещения конца пружины при ее деформации, равна
Так как сила упругости изменяется пропорционально |
A – ? |
деформации, то для вычисления работы можно найти среднее значение ее проекции при изменении деформации пружины от 4 см до 8 см
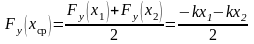 ;
;
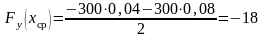 Н.
Н.
Работа силы упругости равна произведению модуля среднего значения силы на модуль перемещения и косинус угла между этими векторами
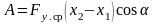 а.
а.
При растяжении пружины вектор силы упругости направлен противоположно вектору перемещения, поэтому угол α между ними равен 180º, а cos α = –1. Тогда работа силы упругости будет равна
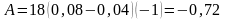 Дж.
Дж.
Работа силы упругости может быть найдена и по изменению потенциальной энергии пружины
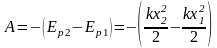 .
.
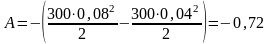 Дж.
Дж.
Ответ: A = – 0,72 Дж.
3. Кран поднимает груз массой 1,5 т на высоту 36 м за 4 мин. Найдите механическую мощность. Силами трения пренебречь.
Дано: m = 1500 кг; h = 36 м; t = 240 с; |
Решение: Механическая мощность равна
Механическая работа A внешних сил при подъеме груза равна изменению его потенциальной энергии (примем начальный уровень h1 = 0) |
N – ? |
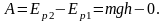
Поэтому механическая мощность равна
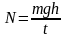 ;
;
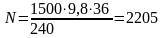 Вт.
Вт.
Ответ: N = 2205 Вт.
4. Самолет Ил-62 имеет четыре двигателя, сила тяги каждого 110 кН. Какова полезная мощность двигателей при полете самолета со скоростью 936 км/ч?
Дано: ʋ = 260 м/с; F = 110000 Н; |
Решение: Полезная мощность N двигателей равна отношению механической работы А ко времени t , |
N – ? |
Механическая работа при совпадении направлений вектора силы и перемещения равна
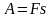 .
.
Отсюда для механической мощности имеем
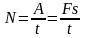 .
.
Так как при равномерном прямолинейном движении
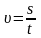 ,
то
,
то
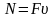 ;
;
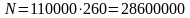 Вт.
Вт.
Ответ: N = 28,6·106 Вт = 28,6 МВт.
5. На высоте 2,5 м от поверхности Земли мяч имел скорость 24 м/с. С какой скоростью будет двигаться мяч у поверхности Земли? Сопротивлением воздуха пренебречь, ускорение свободного падения принять равным 9,8 м/с2.
Дано: ʋ1 = 24 м/с; h1 = 2,5 м; h2 = 0 м; g = 9,8 м/с2; |
Решение: Хотя в условии задачи не указаны направление вектора скорости мяча и масса мяча, задача имеет однозначное решение. Так как на мяч действует только сила тяготения со стороны Земли, к замкнутой системе «Земля – мяч» применим закон сохранения механической энергии. |
ʋ2 – ? |
Согласно этому закону полная механическая энергия системы «Земля – мяч» остается неизменной, а изменение кинетической энергии мяча равно изменению его потенциальной энергии, взятому с противоположным знаком:
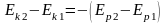 .
.
Обозначим массу мяча m, получим
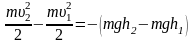 .
.
Разделим обе части равенства на m и умножим на 2
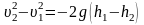 .
.
Отсюда скорость ʋ2 мяча у поверхности Земли равна
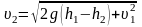 ;
;
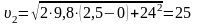 ;
;
Ответ: ʋ2 = 25 м/с.
6. Крупнейшая в мире Саяно-Шушеиская гидроэлектростанция будет вырабатывать 23,5 млрд. кВт·ч электроэнергии в год. Сколько воды должно проходить за год через гидротурбины станции? Высота плотины – 222 м. Считать, что потенциальная энергия воды полностью превращается в электрическую энергию.
Дано: E = 2,35·1010 кВт·ч; ρ = 103 кг/м3; h1 = 222 м; h2 = 0 м; g = 9,8 м/с2; |
Решение: По закону сохранения энергии электроэнергия, вырабатываемая гидроэлектростанцией, получается за счет превращения кинетической энергии движущейся воды в энергию электрического тока. Кинетическая энергия воды, в свою очередь, получается в результате превращения потенциальной энергии воды у вершины плотины в кинетическую у основания плотины. Если не учитывать потери, то вся выработанная гидроэлектростанцией электроэнергия Е равна изменению |
ʋ2 – ? |
потенциальной энергии ΔEp воды, прошедшей через гидроагрегаты станции, взятому с противоположным знаком
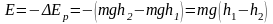 .
.
Массу m воды выразим через ее объем V и плотность ρ
m = ρV.
Из равенств (1) и (2) найдем выражение для объема воды, прошедшей через гидроагрегаты станции
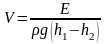 ;
;
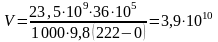 м3
= 39 км3.
м3
= 39 км3.
Ответ: V = 39 км3.
7. Определите минимальное значение тормозного пути автомобиля, начавшего торможение на горизонтальном участке шоссе при скорости движения 63 км/с. Коэффициент трения равен 0,5.
Дано: ʋ0 = 63 км/с; ʋ1 = 0 м/с; μ = 0,5 м; g = 9,8 м/с2; |
Решение: Тормозной путь автомобиля будет иметь минимальное значение при максимальном значении силы трения. Модуль максимального значения силы трения равен
Отсюда найдем модуль ускорения торможения
|
smin – ? |
Вектор
силы трения
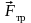 при торможении направлен противоположно
векторам скорости
и перемещения
.
при торможении направлен противоположно
векторам скорости
и перемещения
.
Для определения тормозного пути воспользуемся формулой
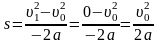 .
.
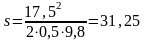 м.
м.
Ответ: smin = 31,25 м.
8. Небольшое тело соскальзывает без трения с вершины неподвижной полусферы радиусом 0,75 м. На какой высоте тело оторвется от поверхности полусферы? Высота отсчитывается от основания полусферы.
Дано: R = 0,75 м; |
Решение: В момент отрыва тело перестает давить на поверхность полусферы – обращается в ноль сила реакции и на тело действует только сила тяжести. |
h – ? |
В то же время, в этот момент движение тела
можно еще считать происходящим по
окружности радиусом R.
Оба эти обстоятельства учитывает
проекция уравнения движения на ось,
проведенную вдоль радиуса от тела к
центру полусферы
то же время, в этот момент движение тела
можно еще считать происходящим по
окружности радиусом R.
Оба эти обстоятельства учитывает
проекция уравнения движения на ось,
проведенную вдоль радиуса от тела к
центру полусферы
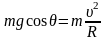 ,
,
здесь θ – угол между этим радиусом и вертикалью. Второе уравнение получим, приравняв энергию в момент отрыва к энергии в начальный момент
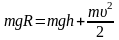
(высота
отсчитывается от поверхности, на которой
лежит полусфера). Выражая υ2
из первого уравнения и учитывая, что
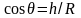 ,
получим
,
получим
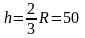 м.
м.
Ответ: h = 50 см.
9. Шар массой 2 кг, имеющий скоростью 6 м/с, абсолютно упруго сталкивается с неподвижным шаром массой 1 кг. Найдите скорость второго шара после удара, считая его центральным.
Дано: m1 = 2 кг; m2 = 1 кг; υ1 = 6 м/с; |
Решение: В случае упругого удара кроме импульса системы сохраняется также ее механическая энергия. Запишем оба закона сохранения
|
u2 – ? |
и сгруппируем члены так, чтобы все, что относится к первому телу, было слева от знака равенства
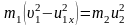 ,
,
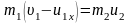 .
.
Если поделить уравнения друг на друга, то получим простое уравнение
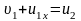 ,
,
Которое вместе с законом сохранения импульса образует систему двух линейных уравнение с двумя неизвестными. При делении уравнений мы, с точки зрения математики, отбросили неинтересное для нас решение начальной системы уравнение: u1x = υ1, u2 = 0. Решив эту систему, получим
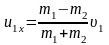 ,
,
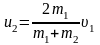 .
.
Отметим, что ответ зависит только от отношения масс шаров и если налетающий шар массивнее (m1 >> m2), он после удара продолжает движение вперед, если легче – откатывается назад, если той же массы останавливается. Подставляя численные данные, находим u2 = 8 м/с.
Ответ: u2 = 8 м/с.
10. Из двух соударяющихся абсолютно упругих шаров шар большей массы покоится. В результате прямого удара меньший шар потерял 3/4 своей кинетической энергии. Во сколько раз масса одного шара больше, чем другого?
Дано: E/E0 = 1/4; |
Решение: Запишем законы сохранения энергии и импульса (с учетом знаков)
|
m2/m1 – ? |
Сгруппируем члены так, чтобы все, что относится к первому телу, было слева от знака равенства
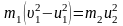 ,
,
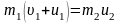 .
.
Если поделить уравнения друг на друга, то получим простое уравнение, которое вместе с законом сохранения импульса даст следующую систему уравнений
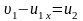 ,
,
.
Если первый шар потерял 3/4 своей энергии, то у него осталось 1/4 часть первоначальной энергии
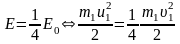 ,
,
откуда получаем соотношение между скоростями
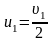 ,
,
важно, что знак уже учтен и u1 > 0. Подставив это выражение в систему и приведя подобные члены, получим
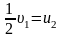 ,
,
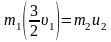 .
.
Отсюда находим
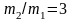 .
.
Ответ: с.

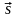 и косинус угла α между вектором
силы и вектором
перемещения
и косинус угла α между вектором
силы и вектором
перемещения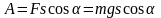 .
.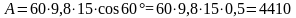 Дж.
Дж.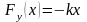 .
.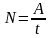 ,
,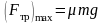 .
.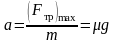 .
.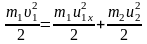 ,
,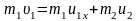
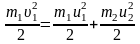 ,
,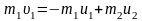 .
.