
- •1.01. Кинематика поступательного и вращательного движения формулы
- •Примеры решения задач
- •1.02. Динамика поступательного движения формулы
- •Примеры решения задач
- •1.03. Закон сохранения импульса тела. Столкновения частиц формулы
- •Примеры решения задач
- •1.04. Закон сохранения энергии формулы
- •Примеры решения задач
- •1.05. Динамика вращательного движения формулы
- •Примеры решения задач
- •1.06. Гармонические колебания формулы
- •Дополнительно. Волны в упругой среде. Акустика
- •Примеры решения задач
- •1.07. Уравнение состояния идеального газа. Молекулярно-кинетическая теория формулы
- •Примеры решения задач
- •1.08. Первое начало термодинамики формулы
- •Примеры решения задач
- •Список используемой литературы
- •Введение
- •Рекомендации по решению задач
- •Требования к оформлению
- •Критерии и шкала оценивания устной защиты решения задач
1.02. Динамика поступательного движения формулы
Ускорение тела:
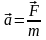 ,
,
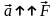 ,
,
здесь m – масса тела, F – сила, действующая на тело;
Второй закон Ньютона:
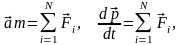
здесь Fi – внешние силы, действующие на тело, p = ma – импульс тела;
Третий закон Ньютона:
 ;
;
Закон всемирного тяготения, сила тяжести, ускорение свободного падения на высоте h над поверхностью Земли, соответственно:
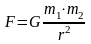 ;
;
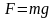 ;
;
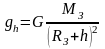 ;
;
здесь G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная, m1,2 – массы взаимодействующих тел, r – расстояние между центрами масс взаимодействующих тел, g = 9,80667 м/с2 – ускорение свободного падения при h = 0, gh – ускорение свободного падения на высоте h, Mз – масса Земли;
Сила упругости:
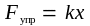 ;
;
здесь k – коэффициент упругости, x – удлинение или сжатие пружины;
Сила трения:
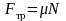 ;
;
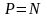 ,
,
здесь μ – коэффициент трения, N – сила реакции опоры, P – вес тела;
Первая космическая скорость на высоте h, первая космическая скорость на поверхности планеты, вторя космическая скорость, соответственно:
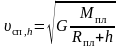 ;
;
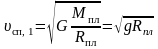 ;
;
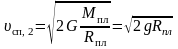 ,
,
здесь υсп,h – скорость спутника планеты на высоте h, Mпл – масса планеты, Rпл – радиус планеты, υсп,1 – первая космическая скорость (скорость искусственного спутника планеты на высоте h = 0), υсп,2 – вторая космическая скорость (скорость, непосредственно у поверхности планеты, необходимая для того, чтобы тело навсегда улетело от планеты);
3-й закон Кеплера:
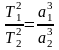 ,
,
здесь T1,2 – периоды обращения двух планет вокруг солнца, a1,2 – большие полуоси орбит планет;
Момент силы:
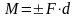 ,
,
здесь d – плечо силы;
Условие равновесия тела:
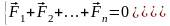 ;
;
Давление:
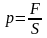 ,
,
здесь F – сила действия на опору, S – площадь поверхности опоры;
Давление в жидкости:
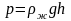 ,
,
здесь ρж – плотность жидкости, g – ускорение свободного падения, h – глубина погружения в жидкость;
Сила Архимеда и вес тела в жидкости:
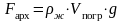 ,
,
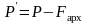 ,
,
здесь ρж – плотность жидкости, Vпогр – объём тела, погружённого в жидкость, g – ускорение свободного падения, P' – вес тела, погружённого в жидкость, P – вес тела.
Примеры решения задач
1. Человек массой 65 кг катается на карусели. Найдите значение силы упругости, действующей на человека при его движении в горизонтальной плоскости со скоростью 12 м/с по окружности радиусом 15 м.
Дано: m = 65 кг; ʋ = 12 м/с; R = 15 м; g = 9,8 м/с2; |
Решение: Движение
человека по окружности, лежащей в
горизонтальной плоскости, происходит
под действием равнодействующей
По второму закону Ньютона модуль равнодействующей равен |
Fy – ? |
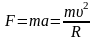
 .
.
Так как вектор перпендикулярен вектору , то вектор является гипотенузой в прямоугольном треугольнике с катетами и . Модуль вектора силы упругости равен
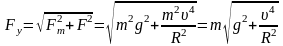 ;
;
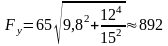 Н.
Н.
Ответ: Fy = 892 Н.
2. Велосипедист массой 90 кг движется со скоростью 12 м/с по вогнутому мосту, траектория его движения является дугой окружности радиусом 30 м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.
Дано: m = 90 кг; ʋ = 12 м/с; R = 30 м; g = 9,8 м/с2; |
Решение: Движение
велосипедиста по дуге окружности
является движением с центростремительным
ускорением
В нижней точке моста вектор центростремительного ускорения |
Fy – ? |
направлен вертикально вверх. Это ускорение по второму закону Ньютона определяется равнодействующей векторов силы тяжести
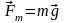 ,
,
направленной вертикально вниз, и силы упругости , действующей со стороны моста и направленной вертикально вверх
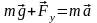 .
.
Направим ось OY вертикально вверх и запишем это уравнение в проекциях на эту ось
 .
.
Проекции
векторов
и
на эту ось положительны, а проекция
вектора
 отрицательна, поэтому уравнение для
модулей сил имеет вид
отрицательна, поэтому уравнение для
модулей сил имеет вид
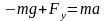 .
.
Отсюда получаем формулу для вычисления модуля силы упругости
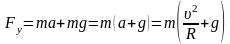 ;
;
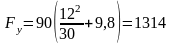 Н.
Н.
Ответ: Fy = 1314 Н.
3. Труба массой 200 кг лежит на двух горизонтальных опорах. Длина трубы 12 м, одна опора находится у конца трубы, вторая на расстоянии 2 м от второго конца трубы. Определите силы реакции опор.
Дано: m = 200 кг; L = 12 м; ℓ = 2 м; g = 9,8 м/с2; |
Решение: Изобразим
все действующие на трубу силы. Сила
тяжести
направлена вертикально вниз и приложена
к центру масс трубы, находящемуся на
равных расстояниях от концов трубы.
Силы реакции опор
|
N1 – ? N2 – ? |
Н аправим
ось OY
вертикально вверх. Тогда для проекций
сил на эту ось имеем равенство
аправим
ось OY
вертикально вверх. Тогда для проекций
сил на эту ось имеем равенство
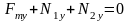 ,
,
а для модулей –
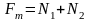 .
.
Так как труба не вращается, алгебраическая сумма моментов всех сил, действующих на нее, равна нулю для любой оси вращения. Выберем в качестве оси вращения горизонтальную прямую, проходящую через центр масс трубы перпендикулярно плоскости чертежа. На основании правила моментов запишем равенство
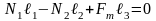 .
.
Так как вектор силы тяжести проходит через ось вращения (ℓ3 = 0), момент этой силы равен нулю. Вектор силы реакции опоры создает вращение против часовой стрелки, поэтому вращательный момент этой силы взят с отрицательным знаком. Таким образом, для решения задачи мы получили систему из двух уравнений
,
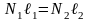 .
.
Решаем эту систему:
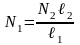 ,
,
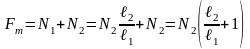 ,
,
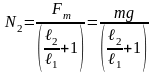 .
.
Из условия задачи следует ℓ1 = L/2 = 6 м, ℓ2 = L/2 – ℓ = 4 м, поэтому
 Н.
Н.
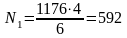 Н.
Н.
Ответ: N1 = 1176 Н, N2 = 592 Н.
4. При падении тела с большой высоты его скорость υуст при установившемся движении достигает 80 м/с. Определите время τ, течение которого, начиная от момента начала падения, скорость становится равной υуст/2. Силу сопротивления воздуха принять пропорциональной скорости тела.
Дано: υуст = 80 м/с; g = 9,8 м/с2; |
Решение: На
падающее тело действуют сила тяжести
|
τ – ? |
Н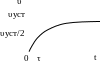 апишем
уравнение движения тела в соответствии
со вторым законом Ньютона в векторной
форме
апишем
уравнение движения тела в соответствии
со вторым законом Ньютона в векторной
форме
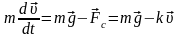 .
.
В проекции на вертикальную ось уравнение примет вид
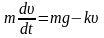 .
.
Разделим переменные и выполним интегрирование от 0 до искомого времени τ
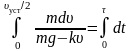 ,
,
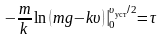 ,
,
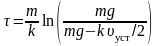 .
.
Коэффициент
пропорциональности найдем из соотношения,
соответствующего установившемуся
движению
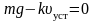 ,
откуда получаем
,
откуда получаем
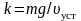 .
После сокращений и упрощений получаем
.
После сокращений и упрощений получаем
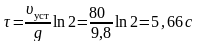 .
.
Ответ: τ = 5,66 с.
5. За сколько секунд маленькая шайба соскользнет с наклонной плоскости высотой 2,5 м и углом наклона к горизонту 60°, если по наклонной плоскости из такого же материала с углом наклона 30° она движется вниз равномерно?
Дано: α1 = 30°; α2 = 60°; h = 2,5 м; g = 9,8 м/с2; |
Решение: Запишем 2-ой закон Ньютона для тела, соскальзывающего с наклонной плоскости
Запишем это уравнение в проекции на ось параллельную наклонной плоскости и ось перпендикулярную наклонной плоскости, соответственно |
t – ? |
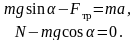

С
учетом выражения для силы трения
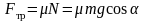 получим выражение для ускорения
получим выражение для ускорения
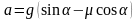 .
.
Коэффициент трения найдем из условия, что при угле наклона α1 = 30° шайба соскальзывает равномерно
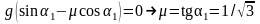 .
.
Время соскальзывания найдем из уравнения кинематики
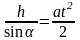 ,
,
В итоге получаем
 .
.
Ответ: t = 1,01 с.

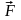 сил тяжести
сил тяжести
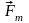 и упругости
и упругости
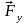 .
Вектор
лежит в горизонтальной плоскости и
направлен к центру окружности.
.
Вектор
лежит в горизонтальной плоскости и
направлен к центру окружности.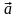 ,
равным по модулю
,
равным по модулю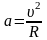 .
. и
и
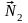 направлены
вертикально вверх. Так как труба не
движется поступательно, геометрическая
сумма векторов сил, действующих на
трубу, равна нулю
направлены
вертикально вверх. Так как труба не
движется поступательно, геометрическая
сумма векторов сил, действующих на
трубу, равна нулю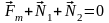 .
.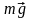 и сила сопротивления воздуха, которая
пропорциональна скорости тела,
и сила сопротивления воздуха, которая
пропорциональна скорости тела,
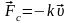 ,
здесь k
– коэффициент пропорциональности.
,
здесь k
– коэффициент пропорциональности.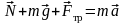 .
.