Примеры решения задач
1. Какое давление на стенки сосудов оказывал бы идеальный газ с концентрацией 100 миллиардов молекул в кубическом миллиметре при средней квадратичной скорости движения молекул 1 км/с и массе молекулы 3·10–27 кг?
Дано: n = 1020 м–3; ʋ = 103 м/с; m0 = 3·10–27 кг; |
Решение: Для вычисления давления идеального газа используем основное уравнение молекулярно-кинетической теории . Подставляя значения величин, взятых в системе СИ, получаем |
p – ? |
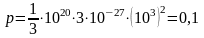0,1
Па.
Давление идеального газа с заданными параметрами оказывается в миллион раз меньше нормального атмосферного давления.
Ответ: p = 0,1 Па.
2. Считая воздух идеальным газом, оцените скорость теплового движения молекул газа при нормальных условиях.
Дано: p = 105 Па; ρ = 1,3 кг/м3; |
Решение: Для решения задачи можно использовать основное уравнение молекулярно-кинетической теории . Так как произведение массы молекулы m0 на концентрацию молекул n равно плотности ρ газа, то давление идеального газа равно |
ʋ – ? |
.
Из этого уравнения следует, что для оценки скорости теплового движения молекул идеального газа можно использовать уравнение (т.е. вычислим среднеквадратичную скорость)
.
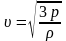Давление воздуха при нормальных условиях равно примерно 105 Па, плотность 1,3 кг/м3. Подставляя эти значения, получаем
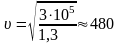м/с.
Ответ: ʋ = 480 м/с.
3. Вычислите среднюю кинетическую энергию молекул идеального при температуре 27 ºС.
Дано: t = 27 ºС; k = 1,83·10–23 Дж/К; |
Решение: Средняя кинетическая энергия Е теплового движения молекул идеального газа связана с абсолютной температурой T газа уравнением
|
E – ? |
,где k – постоянная Больцмана. Для вычисления средней кинетической энергии молекул температуру газа по шкале Цельсия нужно перевести в температуру по абсолютной шкале:
T = t + 273 = 27 + 273 = 300 К.
Подставляя значения температуры и постоянной Больцмана, находим значение средней кинетической энергии молекул идеального газа:
Дж.
Ответ: E = 6,2·10–21 Дж.
4. В баллоне объемом 30 дм3 находится водород под давлением 5·106 Па при температуре 27 ºС. Определите массу газа, считая водород идеальным газом.
Дано: p = 5·106 Па; V = 3·10–2 м3; M = 2·10–3 кг/моль; R = 8,31 Дж/К·моль; T= 300 К; |
Решение: Для решения задачи воспользуемся уравнением состояния идеального газа
Из этого уравнения следует
|
m – ? |
,где М – молярная масса газа; Т – его абсолютная температура. Переведём все величины в СИ и подставим их в расчетную формулу:
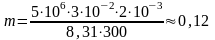кг.
Ответ: m = 0,12 кг.
5. Какой объем занимает 2 моль идеального газа при условиях, соответствующих условиям в фотосфере Солнца? Температура фотосферы 6000 К, давление 1,25·102 Па.
Дано: p = 1,25·102 Па; ν = 2 моль; R = 8,31 Дж/К·моль; T = 6000 К; |
Решение: Для решения задачи используем уравнение состояния идеального газа в форме
Объем газа из этого уравнения равен
|
V – ? |
.Переведём все величины в СИ и подставим их в расчетную формулу:
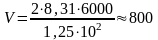м3.
Ответ: V = 800 м3.
6. При температуре 27 ºС и давлении 105 Па объем воздушного шара, заполненного гелием, равен 500 м3. Каким будет объем этого шара, если при подъеме в верхние слои атмосферы температура понизится до –33 ºС, а давление станет равным 5·104 Па? Массу гелия считать постоянной.
Дано: p = 1,25·102 Па; ν = 2 моль; R = 8,31 Дж/(К·моль); T = 6000 К; |
Решение: Из уравнения состояния идеального газа , при
условии m
= const, следует, что
Поэтому выполняется равенство. |
V – ? |
.
.
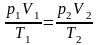Из него получаем
;
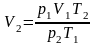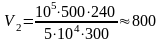м3.
Ответ: V = 800 м3.
7. Вычислите кинетическую энергию теплового движения всех молекул воздуха в физическом кабинете. Объем кабинета – 140 м3, давление воздуха – 105 Па. Сколько воды можно было бы нагреть от 0 до 100 ºС с при полном использовании этой энергии?
Дано: p = 105 Па; V = 210 м3; ΔT = 100 К; c = 4,2·103 Дж/(кг·К); |
Решение: Считая, что свойства воздуха близки к свойствам идеального газа, применим для вычисления кинетической энергии хаотического теплового движения всех его молекул формулу
здесь i – количество степеней свободы, для воздуха i = 5. |
U – ? m – ? |
,Используя уравнение состояния идеального газа
,
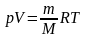запишем выражение для кинетической энергии хаотического движения всех молекул в следующем виде:
,
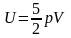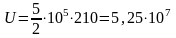Дж.
Для вычисления массы нагреваемой воды запишем уравнение теплового баланса
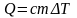
и выразим из него массу m:
.
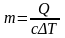По условию задачи Q = U, поэтому масса нагреваемой воды равна
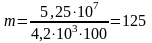кг.
Ответ: m = 125 кг.
8. Как изменится объем пузырька воздуха при всплывании его со дна озера глубиной 10 м к поверхности воды? Температура воды у дна озера и у поверхности одинакова. Атмосферное давление принять равным 105 Па.
Дано: h1 = 20 м; h2 = 0 м; ρ = 1000 кг/м3; g = 9,8 м/с2; T1 = T2; p0 = 105 Па; |
Решение: Объем пузырька воздуха при всплывании будет изменяться из-за уменьшения давления. Так как температура воды одинакова у дна озера и у поверхности воды, изменение объема воздуха будет происходить в результате его изотермического расширения. При изотермическом процессе давление и объем газа связаны соотношением
|
V2/V1 – ? |
.Отсюда
.
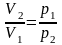Давление p2 у поверхности воды равно внешнему атмосферному давлению p0. Давление p1 на глубине h1 складывается из внешнего атмосферного давления и давления водяного столба: p1 = p2 + ρgh1.
Подставляя численные значения величин, получаем
,
.
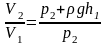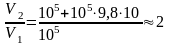Ответ: V2/V1 = 2.
9. По графику процесса, осуществленного с идеальным газом (рис.), постройте графики этого процесса в координатных осях р, Т и V, Т. Температура газа в начальном состоянии 1 была равна 250 К.
Решение:
График на рисунке показывает, что давление газа при переходе из состояния 1 в состояние 2 увеличилось в 3 раза, а объем в течение всего процесса оставался неизменным. Следовательно, процесс изменения состояния газа был изохорным. При изохорном процессе связь между давлением газа р и абсолютной температурой Т выражается уравнением p = p0αT.
Из этого уравнения следует, что отношение давления газа p к абсолютной температуре Т при изохорном процессе является постоянной величиной:
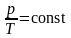или
.
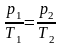Отсюда
;
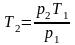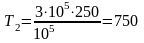К.
По известным начальным и конечным значениям давления и температуры построим в системе координат с осями р, Т точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления р от температуры Т линейная, – следовательно, график изохорного процесса в координатных осях р, Т является прямой, проходящей через точки 1 и 2 (рис.).
В координатных осях V, Т график изохорного процесса – это отрезок прямой, параллельной оси абсцисс, с ординатой, равной объему газа. Концы отрезка определяются прямыми, параллельными оси ординат и проходящими через точки на оси абсцисс, соответствующие значениям начальной и конечной температуры (рис.).
Error: Reference source not found
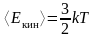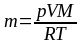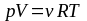
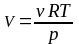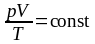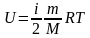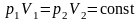