2) Векторная диаграмма. Сложение колебаний одного направления.

Векторная диаграмма.

На оси х отложим вектор

Если привести этот вектор во вращение с , то проекция конца вектора будет перемещаться по ОХ от –а до +а, причем координаты этого вектора изменяются по закону х = аcos(t + _o). Проекция конца вектора а на ОХ будет совершать гармоническое колебание амплитудой равной длине вектора, с круговой частотой равной 𝜔 и с начальной фазой равной углу, образующемся между осью х и вектором а в начальный момент Z.

Рассмотрим сложение двух гармоничных колебаний одинакового направления и частоты:

х = acos(t + _o)

х₁ = a₁cos(t + ₁)

х₂ = a₂cos(t + ₂)

;

Вектор а представляет собой результирующее колебание, вращается с той же угловой скоростью, что и а₁ и а₂, так что результирующее движение будет гармоническим колебанием.

Билет 14.

1)Элементы динамики частиц. Масса. Импульс материальной точки. Импульс системы материальных точек.

Основная задача динамики – найти уравнение движения материальной точки или уравнение движения абсолютно твёрдого тела.

Масса - это скалярная физическая величина, характеризующая меру инертности вещества.

Инерция – явление сохранения состояния покоя или равномерного прямолинейного движения тел в отсутствие внешних воздействий.

Свойство аддитивности:

Вектор импульса материальной точки равен произведению массы на вектор скорости

Пусть задана система N м. т.:

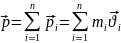
2)Биения. Сложение взаимно перпендикулярных колебаний.

Гармоническое колебание с пульсирующей амплитудой называется биением.

Рассмотрим сложение гармонических колебаний одинакового направления мало отличающихся по частоте

Амплитуды обоих колебаний считаем одинаковыми

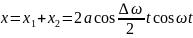
Допустим, что материальная точка может совершать колебания как вдоль Ox, так и вдоль перпендикулярной к ней Oy.

Если возбудить колебания и по Ox и по Oy, то материальная точка будет двигаться по некоторой криволинейной траектории, форма которой будет зависеть от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была = 0.

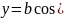
Чтобы получить уравнение траектории необходимо исключить t.

Уравнение эллипса, оси которого повернуты относительно Ox и Oy:

1) Если

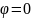
2 ) Если

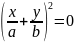
3 ) Если

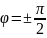
4) Если частоты взаимно перпендикулярных колебаний отличаются на очень маленькую величину, их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз

а) Если соотношение частот 1:2 и разность фаз

б) Если соотношение частот 3:4 и разность фаз

Билет 15.

1) Плотность тел. Сила в механике. Первый закон Ньютона. Второй закон Ньютона. Третий закон Ньютона.

Плотность тел.

Если в-во. распределяется р/м ,то .

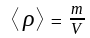А если нет, то .

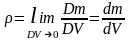Сила в механике.

Сила – является функцией состояния системы, и зависит от координат и скоростей, является векторной величиной .

Cила – мера интенсивности взаимодействия тел, в результате которого они получают ускорения или деформируются.

Сила является мерой взаимодействия не только частиц или тел, но и является мерой взаимодействия тела с окружающими его материальными объектами и силовыми полями.

Первый закон Ньютона.

Любое тело (материальная точка) находится в состоянии покоя или равномерного и прямолинейного движения, если на него не действуют другие тела или действие всех сил скомпенсировано.

Такие тела называют свободными, а их движение свободным движением или движением по инерции.

Второй закон Ньютона.

Второй закон Ньютона устанавливает связь между массой, ускорением его движения и силой, действующей на это тело:

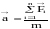где – результирующая сила.

Вектор ускорения прямо пропорционален геометрической сумме векторов всех сил, действующих на м. т. и обратно пропорционален массе этого тела. Направлен в сторону действия результирующей силы.

F_x = ma_x, F_y = ma_y, F_z = ma_z

, .

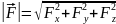
Вектор результирующей силы равен первой производной от вектора импульса м. т. (тела) по времени.

_Если , тогда интегрируя равенство в виде

Получим или .

Изменение импульса тела (материальной точки) зависит от продолжительности действия силы, т. е. зависит не только от величины приложенной силы, но и от времени ее действия.

Третий закон Ньютона.

; .

Силы, с которыми взаимодействуют тела, равны по величине и противоположны по направлению. Линия действия сил лежит на одной прямой, соединяющей центры масс этих тел.

Прямая задача: нахождение по заданным силам состояние движения тел, т. е. вычисление траектории движения.