1) Кинематика вращательного движения. Абсолютно твердое тело. Средняя угловая скорость. Мгновенная угловая скорость.
Абсолютно твердым называют тело, деформациями которого можно пренебречь, а расстояние между любыми его двумя точками сохраняется неизменным при движении.
Вращательным движением абсолютно твердого тела называют движение, при котором все его точки описывают окружности, лежащие в параллельных плоскостях, а центры их лежат на оси вращения
Средняя угловая скорость равна отношению изменения углового перемещения к промежутку времени, за которое перемещение произошло.
= S / R.
– средняя
угловая скорость
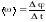
Мгновенная угловая скорость тела равна первой производной углового перемещения по времени.
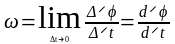
Если
тело вращается равномерно, то
= сonst. Тогда
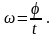
2) Пружинный маятник. Физический маятник. Математический маятник.
Пружинный маятник.
Если колебательная система совершает гармонические колебания, имея одну степень свободы, то она называется линейным классическим гармоническим осциллятором. Примерами классического линейного осциллятора являются пружинный маятник, математический, физический маятники и др.
Гармонические колебания называют свободными, если они совершаются только под действием сил, вызывающих эти колебания.
Найдем дифференциальное уравнение свободных гармонических колебаний пружинного маятника. На маятник действует сила тяжести G = mg
и сила упругости (закон Гука, рис.) Fупр = кх => mg=-kx
;
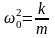T
=
;
.
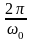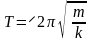Физический маятник.
Твердое тело произвольной формы, свободно совершающее колебания вокруг неподвижной горизонтальной оси, не проходящей через его центр масс, называют физическим маятником.
G=
mgsin;
G
= mgcos;
М =mg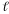
;
M=Lε
=>
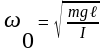период колебаний физического маятника
.
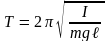Угол отклонения от положения равновесия мал и составляет не более 3-5 градусов, что позволяет в некоторых случаях приравнивать sinφ к φ. Угол φ можно записать, как φ=φ0cos(ωt+α0), φ0 - амплитуда угла φ.
Математический маятник.
Математическим маятником называют материальную точку, закрепленную на невесомой и нерастяжимой нити, совершающую свободные гармонические колебания в вертикальной плоскости.
;
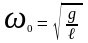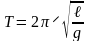
Период колебания математического маятника прямо пропорционален квадратному корню длины маятника и обратно пропорционален квадратному корню ускорения силы тяжести.
Билет 12.
1)Связь линейной и угловой скоростей. Период и частота вращения. Среднее угловое ускорение.
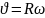
Период – время, за которое тело совершает полный оборот вокруг оси или полюса
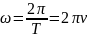
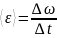
2)Затухающие гармонические колебания. Основные параметры затухающих колебаний.
Колебания называют затухающими, если убыль энергии физической системы не восполняется в процессе ее колебательного движения.
Кроме квазиупругой силы, вызывающей колебания, на частицу действуют силы сопротивления (трения) со стороны окружающей среды.
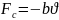
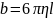
b – коэффициент сопротивления окружающей среды; l – характерный размер тела
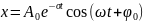
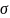– коэффициент
затухания колебаний
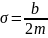
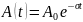
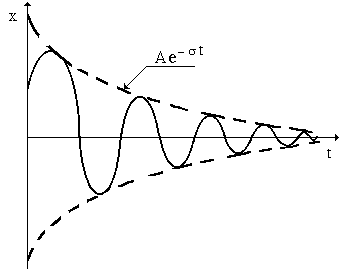
Коэффициент затухания колебаний физической системы прямо пропорционален коэффициенту сопротивления окружающей среды и обратно пропорционален массе системы. Характеризует быстроту затухания свободных колебаний.
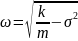
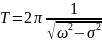
Декремент затухания:
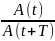
Логарифмический декремент затухания:
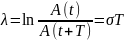
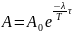
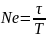
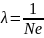
Логарифмический декремент затухания обратно пропорционален числу колебаний, совершаемых за то время, за которое A уменьшается в e раз.
Для характеристики колебательной системы часто используется величина, называющаяся добротностью:
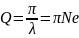
Энергия колебательного процесса:
Билет 13.
1) Мгновенное угловое ускорение. Связь линейного и углового ускорений. Связь линейных величин s, v, a c угловыми , , .
Мгновенное угловое ускорение.
Мгновенное угловое ускорение численно равно первой производной угловой скорости по времени или – второй производной углового перемещения по времени.
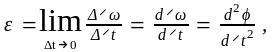
𝜔=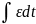
;
𝜑=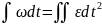
;
Связь линейного и углового ускорений.
;
;
=
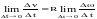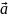
R
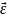
В СИ единицей измерения углового ускорения является радиан на секунду в квадрате (рад/c2 или с-2)
Связь линейных величин s, v, a c угловыми , , .
s = R
v = R
a = R
аn
=
=
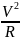2
R