2) Силы трения. Энергия упругой деформации.

Появляются при перемещении соприкасающихся тел или их частей друг относительно друга.

Трение, возникающее при относительном перемещении 2х соприкасающихся тел, называется внешним.

Трение между частями одного и того же сплошного тела носит название внутреннего тела.

Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упругодеформированное тело. В этом случае энергия зависит от взаимного расположения отдельных частей тела.

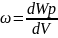– удельная энергия

Билет 6.

1) Вектор перемещения материальной точки. Прямолинейное равномерное движение.

Вектор перемещения – это вектор, проведённый из начального положения материальной точки в конечное.

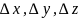– изменение координат за соответствующий промежуток времени.

Если материальная точка одновременно участвует в нескольких перемещениях, то, согласно принципу независимости движений, каждое совершается независимо от другого.

Движение называют равномерным и прямолинейным, если материальная точка движется вдоль прямой с постоянной по величине и направлению скоростью. В этом случае средняя и мгновенная скорости совпадают.

2) Кинематика движущейся жидкости. Идеальная жидкость. Уравнение Бернулли.

Л инию, касательная к которой указывает направление скорости движения частицы, проходящей в рассматриваемый момент времени через эту точку касания, называют линией тока.

Если поле скоростей и соответствующие ему линии тока, не изменяются с течением времени, то движение жидкости называют стационарным.

Они образуют поверхность, называемую трубкой тока.

Скорости частиц жидкости направлены по касательным к линиям тока.

Массу жидкости, протекающую через поперечное сечение трубки тока за время dt, можно определить по формуле

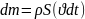
Для сечений трубки тока при стационарном течении жидкости dm = сonst.

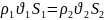
Если жидкость несжимаема, то

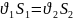
Скорость течения жидкости обратно пропорциональна площади поперечного сечения трубки тока.

Идеальная жидкость:

Вследствие малой сжимаемости жидкости во многих случаях можно полностью пренебречь изменением ее объема, т. е. можно говорить об абсолютно несжимаемой жидкости.

Ж идкость, в которой при любых движениях не возникают силы внутреннего трения, называют идеальной.

Рассмотрим стационарное движение идеальной жидкости в потенциальном поле сил (например, поле силы тяжести). Работа, совершаемая силами давления при перемещении некоторой массы жидкости:

Уравнение Бернулли:

– удельная энергия,

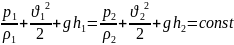
Билет 7.

1) Средняя скорость материальной точки. Мгновенная скорость.

Вектором средней скорости называют физическую величину, равную отношению вектора перемещения (приращению радиус-вектора) к промежутку времени, за которое это перемещение произошло.

;

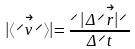Если материальная точка движется по окружности или по любой замкнутой траектории, то есть через некоторое время приходит в исходное положение, то её перемещение равно 0.

Средняя скалярная скорость определяется отношением отрезка пути пройденного материальной точкой по траектории за некоторый промежуток времени к величине этого промежутка.

<V_c> =

Если м.т. совершает ряд последовательных перемещений , .. 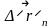, то вектор средней скорости результирующего перемещения находят по формуле

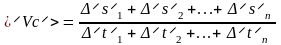- средняя скорость

Часто при решении задач для нахождения средней скорости используют формулу <v> =

Эта формула справедлива в случае прямолинейного равноускоренного или равнозамедленного движения в одну сторону, т.е. без изменения направления скорости.

Вектор мгновенной скорости равен пределу отношения приращения радиус-вектора м. т. к тому промежутку времени, за которое это приращение произошло.

Мгновенная скалярная ск-ть:

Проекций вектора скорости на оси координат:

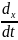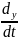V_x = , v_y = , v_z = ;

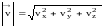
Таким образом, вектор V характеризует быстроту изменения перемещения в пространстве по величине и направлению с течением времени.

V – это функция по времени.

V=f(t); V=V(t)