1)Момент импульса материальной точки.
Вектором
момента импульса м.т. относительно
полюса называют векторное произведение
радиус-вектора
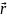и вектора импульса
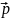относительно этого же полюса.
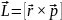
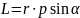
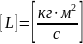
2)Уравнение состояния идеального газа (уравнение Клапейрона, уравнение Менделеева-Клапейрона). Закон Авогадро. Закон дальтона.
Флуктуациями называют случайное отклонение физической величины от её среднего значения.
Идеальным называют газ, взаимодействием между молекулами которого можно пренебречь.
Уравнение Клапейрона устанавливает зависимость между параметрами ИГ.
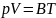
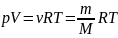
Из уравнения состояния ИГ следует:
1)Закон Авогадро: в равных объёмах различных газов, находящихся при одинаковых давлении и температуре, содержится одинаковое количество молекул равное постоянной Авогадро.
2)Закон Дальтона: в состоянии теплового равновесия давление в смеси химически не взаимодействующих ИГ равно сумме парциальных давлений отдельных газов, входящих в смесь.
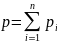
Парциальное давление — давление, которое имел бы газ, входящий в состав газовой смеси, если бы он один занимал объём, равный объёму смеси при данной температуре.
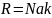
Билет 21.
1) Момент импульса системы материальных точек. Связь вектора момента силы и вектора момента импульса.
Момент импульса системы материальных точек.
Вектор момента импульса системы м. т. (тела) относительно полюса 0 равен геометрической сумме векторов моментов импульса, действующих на каждую м. т. в отдельности относительно того же полюса 0
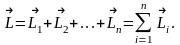
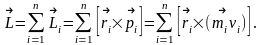
I = mr2 – момент инерции системы материальных точек.
U=R (R=r)
L = I
Связь вектора момента силы и вектора момента импульса.
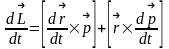
Согласно
2-му закону Ньютона
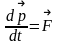
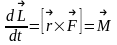
Выражение
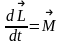устанавливает связь между вектором
момента импульса и вектором момента
силы в инерциальной системе отсчета.
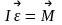
2) Давление в молекулярно-кинетической теории. Распределение энергии молекул идеального газа по степеням свободы. Внутренняя энергия.
Давление в молекулярно-кинетической теории.
Взаимное столкновение в молекуле газа происходит чаще, чем их соударения со стенками сосудов, в которых находится газ. Будем учитывать только столкновение молекул со стенками сосуда, в котором заключен идеальный газ.
Молекулы идеального газа можно рассматривать как материальные точки, не взаимодействующие между собой и движущиеся прямолинейно и равномерно между каждыми двумя последовательными соударениями со стенками сосуда.
,
-
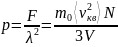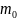масса одной молекулы, N
– число молекул
=>
,
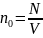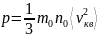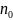– концентрация
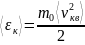
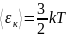
I. Вывод: с точки зрения МКТ р газа прямо пропорционально концентрации молекул газа и его абсолютной температуре.
II.
Вывод:
идеального
газа прямо пропорциональна абсолютной
температуре.
Распределение энергии молекул идеального газа по степеням свободы.
Каждая одноатомная молекула имеет 3 поступательные степени свободы.
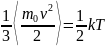
В
состоянии термодинамического равновесия
на каждую степень свободы движения
частиц вещества (колебательного,
вращательного, колебательного) приходится
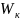в среднем равная
;
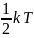
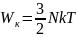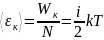
Внутренняя энергия.
Включает в себя энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов) и энергию взаимодействия этих частиц, т.е. кинетическую и потенциальную, за исключением суммарной энергии покоя всех частиц.
Свойства внутренней энергии:
1. Внутренняя энергия является функцией состояния физической системы.
2. Внутренняя энергия физической системы не зависит от пути перехода её из одного состояния в другое, определяется только значением внутренней энергии в начальном и конечном состоянии.
,
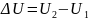U
характеризуется свойством аддитивности
(равна суммарной внутренней энергии
тел, входящих в систему).
Каждый атом обладает средней энергией 𝜀к
U=N
=
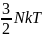
Uвр=
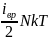
Uкол=
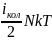
U = Uпост + Uвр + Uкол
U
=
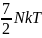
Каждое колебательное движение молекулы характеризуется средней кинетической и потенциальной энергией, которые равны между собой.
ν=
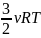U=
=> U=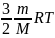
Вывод: из-за отсутствия взаимодействия между молекулами идеального газа его U зависит от числа частиц, температуры и не зависит от объема.
Билет 22.