5. Метод векторных диаграмм

На оси Х выберем начало отсчета (точка 0) и отложим вектор длиной , образующий с осью угол _о. Приведем этот вектор во вращение против часовой стрелки с циклической частотой  (рис. 5).

При этом проекция на ось Х конца вектора будет периодически совершать движение вдоль оси Х в пределах от А до +А, т. е. координата этой проекции будет изменяться по гармоническому закону:

х = А cos(t + _o).

Рис. 5

Если система одновременно участвует в нескольких колебаниях, то решение задачи значительно упрощается и становится наглядным при использовании метода векторных диаграмм (метод вращающего вектора на плоскости).

Особенно этот метод эффективен при сложении двух и более гармонических колебаний.

Вывод: проекция конца вектора на произвольную ось (например, ось Х) будет совершать гармонические колебания с амплитудой, равной длине вектора, циклической (круговой) частотой, равной угловой скорости вращения вектора, и начальной фазой, равной углу, образованному данным вектором с осью в начальный момент времени.

1.6. Сложение колебаний одного направления

Рис. 6

На практике довольно часто встречаются тела, которые одновременно участвуют в двух колебаниях, происходящих вдоль одного направления. Например, груз закреплен на пружине к потолку движущегося вагона, который сам совершает колебания в вертикальной плоскости (рис. 6), или груз, который закреплен на двух последовательно соединенных пружинах с различными коэффициентами жесткости. Допустим, что колебания груза на пружине совершаются по закону

х₁ = А₁cos(t + _o1). (5)

Колебания вагона совершаются по закону

х₂ = А₂cos(t + _o2). (6)

Представим оба колебания с помощью вращающих векторов и одинаковой круговой частотой  (рис. 7). Используя правила сложения векторов, построим результирующий вектор

. (7)

Проекция результирующего смещения х равна сумме отдельных проекций смещений грузов: х = х₁ + х₂ . (8)

Следовательно, действительно х представляет собой результирующее гармоническое колебание амплитуды А, циклической частоты  и начальной фазы _о, т. е.

х = А cos(t + _o). (9)

Для того чтобы написать уравнение результирующего гармонического колебания тела, одновременно участвующего в двух одинаково направленных гармонических колебаниях, необходимо знать амплитуду результирующего колебания и его начальную фазу.

Рис. 7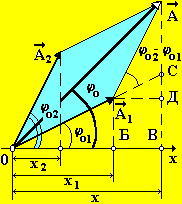

В соответствии с рис. 7 и теоремой косинусов для результирующей амплитуды, имеем следующее равенство:

А² = A₁² + А₂² + 2А₁А₂cos(_o2  _o1). (10)

Используя тригонометрические функции синуса, косинуса и тангенса (рис. 7), найдем начальную фазу результирующего гармонического колебания в виде:

. (11)

Анализ уравнения (10) показывает, что величина результирующей амплитуды зависит от разности фаз складываемых колебаний. В связи с этим возможны два случая: