11. Формула Стокса

Рассмотрим движение тела в жидкости (например, при осаждении мелких частиц – седиментации). На частицу радиуса R при осаждении действуют три силы: сила тяжести , сила сопротивления среды и сила Архимеда (рис. 14).

Для описания движения частицы относительно жидкости используется число Рейнольдса

Рис. 14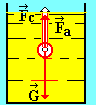

, (62)

где v – cкорость частицы, R – ее характерный размер.

Замечание: Это число Рейнольдса отличается от числа Рейнольдса в случае течения жидкости, например, в трубе, т. к. относится к различным явлениям.

Если число Рейнольдса много меньше единицы (для малых частиц, порошков и т. д., имеющих размеры порядка 0,1–0,05 мм и меньше), то обтекающий частицу поток жидкости является ламинарным.

При этом сила сопротивления F_c = bv , где b – коэффициент, зависящий от размеров и формы частицы и от вязкости жидкости.

Для частиц сферической формы радиуса r

b = 6R. (63)

Следовательно, сила сопротивления будет иметь вид (формула Стокса)

F_c = 6Rv. (64)

При наличии турбулентности сила сопротивления F_c ~ v², а число Рейнольдса заключено в интервале (1–10). Формула (64) применяется для расчетов при проведении ряда физических опытов: определение заряда электрона методом Милликена, при изучении броуновского движения и т. п.

13. Разрывные течения. Подъемная сила крыла

Рассмотрим силовые действия потока жидкости или газа на помещенные в них тела. Силу F, действующую со стороны потока на тело, можно разложить на две составляющие: одну в направлении потока (F_х) и вторую (F_y) – перпендикулярную потоку. Сила F зависит от формы и размеров тел, от ориентации тела относительно потока, относительно скорости потока и свойств жидкости. Силу F_x называют лобовым сопротивлением.

Силу F_y – подъемной силой, которая, например, действует на крылья самолетов или морских судов на подводных крыльях. Эта сила может быть направлена как вверх, так и вниз, в зависимости от ориентации крыльев относительно направления движения. Лобовое сопротивление слагается из двух сил: силы, возникающей за счет разности давлений на переднюю и заднюю поверхности тела, и вязких сил внутреннего трения.

При больших числах Рейнольдса (большие скорости движения) преобладают силы за счет разности давлений, при малых числах Рейнольдса – силы внутреннего трения. В дальнейшем в основном будем рассматривать стационарное течение идеальной жидкости. Если нет внешних сил, то жидкость течет параллельным потоком. При внесении в жидкость тела нарушается параллельность потока вблизи него.

Но на достаточно больших расстояниях от тела поток остается параллельным. По истечении некоторого времени движение жидкости устанавливается.

Рис. 18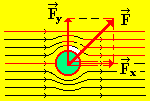

Если тело в такой жидкости движется равномерно, то при стационарном течении идеальной жидкости лобовое сопротивление будет равно нулю (парадокс Даламбера). Этот вывод относится только к лобовому сопротивлению, но не подъемной силе и моменту силы, с которым поток жидкости действует на тело.

Момент сил, относительно центра масс, равен нулю, когда тело симметрично и расположено симметрично относительно потока. Если тело движется с ускорением, то парадокс Даламбера не возникает.

Парадокс Даламбера легко объясняется, если рассмотреть распределение линий тока. Линии тока при стационарном обтекании шара или цилиндра идеальной жидкостью, они симметричны, а скорости частиц жидкости в соответствующих точках перед, и за телом, равны по величине и отличаются только направлением. В уравнение Д. Бернулли скорость входит в квадрате.

Следовательно, распределение давления в потоке перед телом и за телом одинаково. Давление на переднюю поверхность тела уравновешивается давлением на заднюю поверхность, сила лобового сопротивления равна нулю.

Сила лобового сопротивления всегда направлена по течению, поэтому при обращении течения она должна изменить знак, следовательно, F_х = 0.

К подъемной силе это не применимо, так как нет оснований, утверждать, что при обращении направления потока должна изменить направление и подъемная сила. При стационарном течении жидкости поток ее является непрерывным. Однако в некоторых случаях уравнения гидродинамики допускают и такие стационарные течения, в которых скорость жидкости испытывает разрыв непрерывности, что было исследовано впервые Кирхгофом.

Так как в идеальной жидкости при любых движениях не могут возникать касательные силы, то возможны разрывные течения, в которых касательные составляющие скорости течения жидкости претерпевают разрыв на некоторой поверхности (неподвижной или движущейся). Такие течения называют тангенциальными разрывами, которые в несжимаемой жидкости гидродинамически неустойчивы.

Зависимость величины подъемной силы от циркуляции скорости была установлена Жуковским и Кутта.

Согласно теореме Жуковского о циркуляции скорости для крыла, формула подъемной силы имеет вид

F_y = vГ, (74)

где  – плотность воздуха;  – длина крыла; v – скорость потока; Г – циркуляция скорости по замкнутому контуру, охватывающему крыло.

Циркуляция скорости по замкнутому контуру, охватывающему крыло,

, (75)

где d – длина хорды;  – угол атаки.

Углом атаки называют угол между направлением потока и хордой крыла (рис. 20).

Подъемную силу часто записывают в виде:

, (76)

где S – площадь сечения крыла (миндаль); С_у – коэффициент подъемной силы, безразмерная величина, зависящая от числа Рейнольдса Re, от отношения длины крыла к его хорде и угла атаки.

Силу лобового сопротивления находят по формуле

(77)

Рис. 21

где S – площадь сечения минделя; С_х – коэффициент лобового сопротив-ления, безразмерная величина; является функцией числа Рейнольдса и учитывает свойства среды и форму тела.