После интегрирования выражения (54), получим

.

Постоянную интегрирования С определим из условия, что на стенке трубы скорость течения жидкости должна обращаться в нуль при r = R, т. е.

. (55)

Из формулы (55) следует, что скорость течения жидкости будет максимальной на оси трубы при r = 0:

.

При удалении от оси трубы скорость течения изменяется по параболическому закону.

Определим ежесекундный расход жидкости при протекании ее через поперечное сечение трубы.

Массу жидкости, протекающую за одну секунду (расход жидкости) через сечение с внутренним r и внешним r + dr радиусами трубы, запишем в виде:

Рис. 13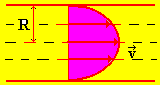

dQ= 2rdrv. (56)

Подставим значение скорости v из формулы (55) в (56).

Тогда полный расход жидкости

.

После интегрирования получим формулу Пуазейля:

. (57)

Вывод: расход жидкости прямо пропорционален разности давлений на входе и выходе трубы, четвертой степени ее радиуса, плотности жидкости; обратно пропорционален коэффициенту вязкости и длине трубы.

12. Потенциальное и вихревое движения

Согласно классической механике, все движения жидкостей разделяются на потенциальные и вихревые.

Рис. 15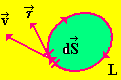

Рассмотрим поле скоростей жидкости v(r) в некоторый фиксированный момент времени. Выделим в жидкости произвольный замкнутый контур L, с указанием направления обхода. Введем единичный вектор касательной и элемент длины контура L, взятые в положительном направлении.

Циркуляцией вектора скорости по замкнутому контуру L называют интеграл

(65)

или . (66)

Если циркуляция вектора скорости по любому замкнутому контуру не обращается в нуль, то движение жидкости называют вихревым. Определение потенциальности течения жидкости аналогично определению консервативных сил.

Следовательно, при потенциальном течении линейный интеграл , взятый вдоль незамкнутой кривой, соединяющий точки А и Б, зависит только от координат этих точек, но не зависит от формы кривой АБ.

По аналогии с потенциальной энергией можно ввести функцию координат , через которую скорость определяется формулой

= grad , (67)

где  – потенциал скоростей.

Всякое течение идеальной жидкости, возникающее из состояния покоя под действием консервативных сил, является потенциальным. Примером потенциального течения является течение жидкости вдоль параллельных прямых линий с постоянной скоростью. Примером вихревого движения является плоское течение, в котором жидкость вращается по концентрическим окружностям с постоянной угловой скоростью . Циркуляция скорости по окружности радиуса R в этом случае

Г = 2R². (68)

Отношение

(69)

не зависит от радиуса R. Если угловая скорость вращения жидкости зависит от радиуса, то берут предел этого отношения при R 0, т. е.

. (70)

Следовательно, этот предел равен удвоенному значению угловой скорости, с которой вращаются частицы жидкости вблизи оси 0, и называется вихрем, или ротором скорости v, т. е.

. (71)

Рис. 17

Если ротор скорости v известен в каждой точке жидкости, то можно найти циркуляцию скорости по любому замкнутому контуру, интегрируя значение ротора скорости v в каждой точке, лежащей внутри контура. Рассмотрим движение идеальной жидкости.

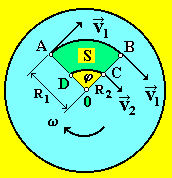
Пусть эта жидкость находится во вращающемся сосуде. Если она вращается вместе с сосудом как твердое тело, то частицы, расположенные на расстоянии R от оси сосуда, будут иметь скорость v = R.

Такое твердотельное распределение скорости легко получить, если жидкость заморозить и привести во вращение с угловой скоростью , а затем ее разморозить.

Используя, найдем ротор скорости в некоторой точке.

Циркуляция скорости по контуру ABCD

Г =  (R₁v₁ – R₂v₂) =   (R₁² – R₂²).

Площадь этого контура

.

Следовательно,

и .

Теперь рассмотрим течение идеальной жидкости с таким распределением скоростей, для которого в каждой точке .

В этом случае свойство потенциальности сохраняется с течением времени, что является следствием закона сохранения момента импульса.

Однако потенциальность поля скоростей еще не означает отсутствие вихревого движения.

Например, рассмотрим воронку водоворота.

При удалении от его центра скорость убывает обратно пропорционально расстоянию:

где А – некоторый параметр, характеризующий мощность вихря, а циркуляция скорости по любому замкнутому контуру равна нулю.

Следовательно, в каждой точке и течение жидкости в водовороте потенциально, за исключением центра воронки водоворота.

Циркуляция скорости по любому контуру вокруг него не зависит от выбора контура и равна Г = 2A, а ротор вектора скорости в этой точке бесконечно велик.

Оценим энергию W, приходящуюся на единицу длины такого вихря. Для этого просуммируем кинетическую энергию W_k, т. е.

(72)

где dV – бесконечно малые объемы жидкости, находящиеся на расстоянии r от оси вихря по всему объему сосуда;  – плотность жидкости.

Если характерный размер сосуда 2R, то

. (73)