8. Гидродинамика вязкой жидкости

При движении реальной жидкости (газа), кроме сил нормального давления, между движущими ее слоями действуют касательные силы внутреннего трения (вязкости).

Рис. 11

Согласно уравнению Д. Бернулли (7.24) при течении жидкости по горизонтальной, прямой трубе постоянного сечения, в которой отсутствуют силы внутреннего трения, при стационарном режиме, давление жидкости одинаково по всей длине трубы.

При течении вязкой жидкости давление падает в направлении ее течения (рис. 11).

Для осуществления стационарного течения жидкости на концах трубы необходимо поддерживать постоянную разность давлений, которая уравновешивается силами внутреннего трения, возникающими при ее течении. Если жидкость находится во вращающемся сосуде, то постепенно она также приходит во вращение.

Сначала начинают вращаться слои жидкости, прилегающие к стенке сосуда (за счет сил внешнего трения), затем вращение передается внутренним слоям (за счет сил внутреннего трения).

Вращение происходит при возникновении касательных сил между стенкой сосуда и жидкостью и между слоями жидкости, вращающимися с различными угловыми скоростями, пока вся жидкость не начнет вращаться, как твердое тело.

Природа сил внутреннего трения рассмотрена в разделе «Вязкость». Здесь же остановимся только на количественных законах внутреннего трения.

Для равномерного перемещения подвижной пластины со скоростью v необходимо к ней приложить постоянную силу, направленную в сторону течения жидкости.

В этот момент на неподвижную пластину будет действовать равная по величине, но противоположно направленная сила, чтобы удержать ее в покое.

Сила внутреннего трения

, (48)

где  – коэффициент вязкости, зависит от вещества жидкости и ее температуры, но не зависит от материала пластины; S – площадь пластины; h – расстояние между пластинами.

Если обе пластины движутся: верхняя – со скоростью v₁, нижняя – со скоростью v₂, то формула (48) принимает вид

. (49)

При движении жидкости в направлении оси Х со скоростью v_x, которая зависит только от координаты у [т. е. v_x = v_x(y), v_y = v_z = 0], действует касательная сила _ух (индекс у указывает направление внешней нормали к верхней границе слоя, индекс х – направление действия силы) на единицу площади верхней границы слоя, со стороны вышележащих слоев жидкости.

Следовательно,

, (50)

где

_ух = F/S.

Формула (50) справедлива для любого вида движения, причем касательные напряжения действуют не только в направлении течения жидкости, но и в плоскости, перпендикулярной течению, т. е.

_ух = _ху.

9. Формула Пуазейля. Течение жидкости по трубе

При течении вязкой несжимаемой жидкости по цилиндрической трубе радиуса R линии тока ее параллельны оси трубы.

Выделим произвольную бесконечно узкую трубку тока.

Рис. 7.17

Из условия не сжимаемости жидкости следует, что скорость течения v будет постоянной вдоль всей трубки тока, но

Рис.12

может изменяться по мере удаления от оси трубы, т. е.

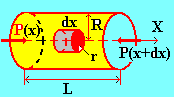
v = f(r),

где r – расстояние от оси трубы.

Выделим в трубе произвольный бесконечно малый цилиндрический элемент длины dx и радиуса r.

Ось Х совпадает с направлением течения жидкости и направлена вдоль оси трубы.

В направлении течения жидкости на боковую поверхность действует касательная сила внутреннего трения

(51)

где  – коэффициент вязкости; L – длина трубы.

На оба основания цилиндра в том же направлении действует сила разности давлений

(52)

В случае стационарного течения жидкости результирующая сумма этих сил равна нулю, т. е.

. (53)

Скорость v(r) = сonst и ее производная

.

Следовательно, должна быть постоянной и производная

т. е.

,

где Р₁, Р₂ – давления на входе и выходе трубы, соответственно.

Таким образом,

. (54)