4

Механика твердого тела

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________

1. Момент инерции материальной точки

Моментом инерции м. т. относительно полюса называют скалярную величину, равную произведению массы этой точки на квадрат расстояния до полюса.

Момент инерции м. т. можно найти по формуле

I₀ = mR², (1)

где m – масса м. т.; R – расстояние до полюса О.

Единицей измерения момента инерции в СИ является килограмм, умноженный на метр в квадрате (кгм²).

2. Момент инерции системы материальных точек

Тело можно представить состоящим из большого числа м.т., поэтому момент инерции системы м. т.

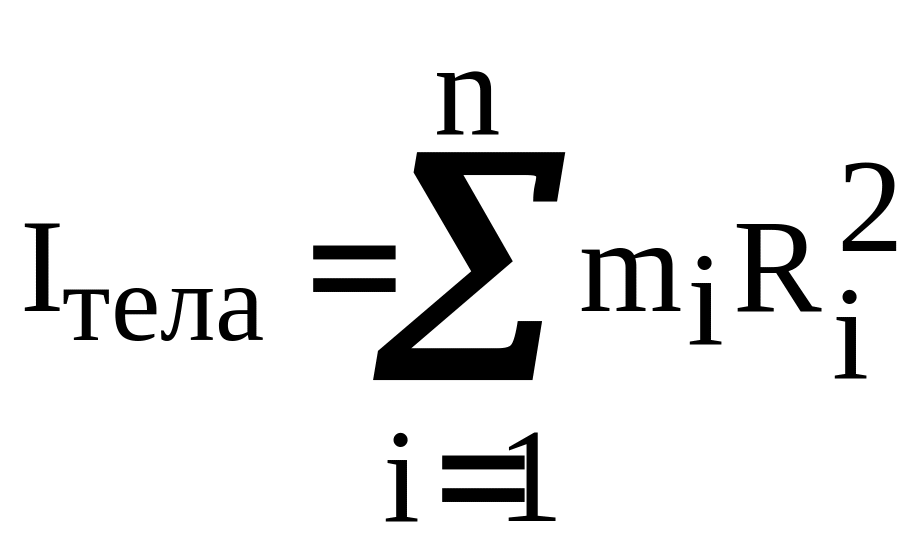, (2)

где m_i – масса i-й м. т.; R_i – ее расстояние до полюса 0.

Моментом инерции системы м. т. или тела относительно полюса (точки) называют алгебраическую сумму произведений масс м. т., из которых состоит тело, на квадрат расстояния их до полюса 0.

При непрерывном распределении массы по объему тела момент инерции относительно полюса находится по формуле

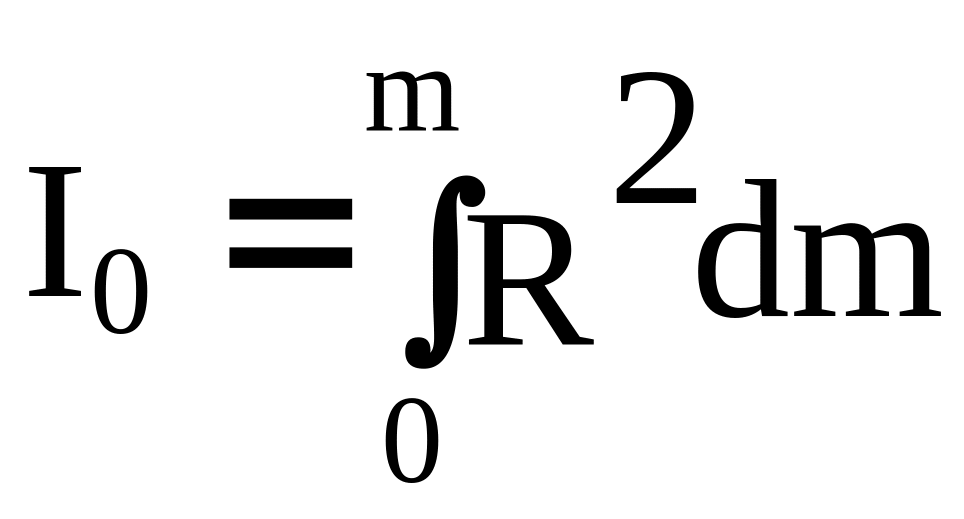(3)

В случае момента инерции относительно полюса массу dm умножают на квадрат расстояния до неподвижной точки (полюса), а в случае момента инерции относительно оси – до неподвижной оси.

В декартовой системе координат сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающих в одной точке 0, равна удвоенному моменту инерции этого тела относительно этого же начала:

I_x + I_y+ I_z = 2I₀ . (4)

3. Теорема Штейнера

Для установления связи между моментом инерции тел относительно двух параллельных осей применяется теорема Штейнера (Штейнера –Гюйгенса):

I = I_c + md². (5)

Момент инерции тела относительно произвольной оси равен моменту инерции относительно оси, параллельной данной, проходящей через центр масс, плюс произведение массы тела на квадрат расстояния между осями.

4. Момент инерции однородного стержня

Моменты инерции различных тел можно найти по формуле I = mR²,

где m – коэффициент пропорциональности, который зависит от формы тела и его расположения относительно оси вращения.

Найдем момент инерции однородного стержня относительно оси, проходящей через один из его концов, перпендикулярно продольной геометрической оси симметрии. Пусть ось вращения проходит через правый конец стержня, тогда I = mmL², где L - длина стержня.

Согласно теореме Штейнера, имеем .

Рис. 2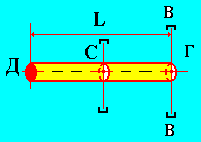

Величину момента инерции I_c относительно оси, проходящей через центр масс, представим как сумму моментов инерции двух стержней с длинами L/2 и массой каждого, равной m/2 стержня, т. е.

.

Подставим значения момента инерции I и I_c в формулу теоремы Штейнера – Гюйгенса и найдем : .

После преобразования получим, что m = 1 / 3.

Следовательно, момент инерции стержня относительно оси, проходящей через центр масс, (6)

относительно оси (7)

5. Момент инерции сплошного шара

Рис. 3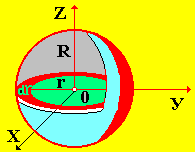

Сплошной однородный шар можно представить как сумму бесконечно тонких сферических слоев с массами dm = mdV/V. Объем сферического слоя dV представим в виде: dV = 4r²dr, где r – радиус сферического слоя. Объем шара V = 4/3R³, где R – радиус шара. Если шар полый, то момент инерции сферического слоя относительно его центра масс ^I_c ^{= mR2, но ,} где из-за симметрии I_x = I_y = I_z. ^{Момент инерции сферического слоя относительно диаметра .}

Тогда момент инерции шара

5.1. Примеры моментов инерции некоторых тел

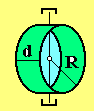
4. Тонкое кольцо радиусом R

и шириной d.

однородного состава относительно оси

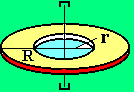
3. Полый цилиндр с внутренним r и внешним R радиусами

.

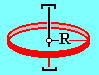
2. Тонкое кольцо

радиуса R

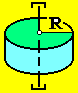
1. Сплошной

цилиндр радиуса R

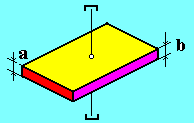
5. Тонкий параллелепипед

6. Работа, совершаемая телом при вращательном движении

Если произвольная м. т. вращается по окружности и на нее действует сила , то при повороте на некоторый угол совершается элементарная работа

А = F ds, где ds = r d.

Тогда А = (r F) d = M d. (8)

Полученное выражение остается справедливым и случае системы м.т. (твердых тел), совершающих вращательное движение относительно оси Z при  = сonst. В этом случае момент внутренних сил равен нулю и работа не совершается. Для нахождения полной работы необходимо вычислить интеграл:

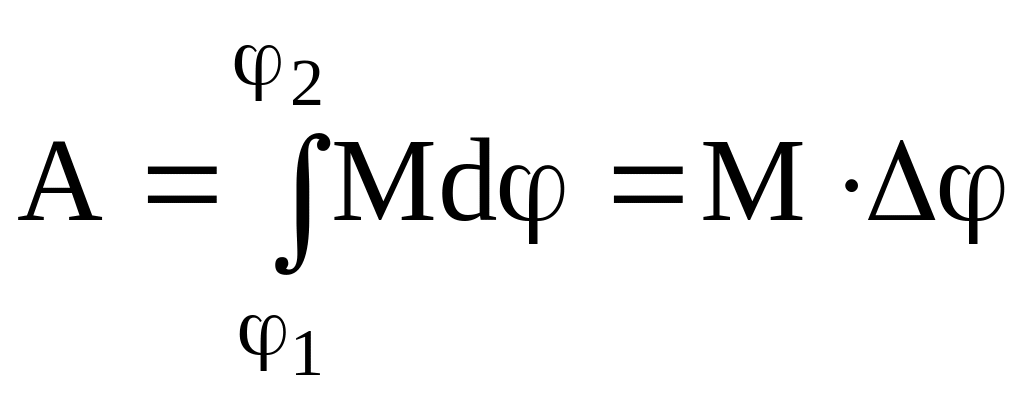, (9)

где  = ₂  _1.

Если действующая сила является потенциальной, то А =  dWp ,

где dWp  бесконечно малое изменение потенциальной энергии тела при повороте на малый угол dj, т. е.

dWp =  M_zd или M_{z =}  dWp/d .

7. Кинетическая энергия тела, совершающего

вращательное движение

Кинетическая энергия м. т. W_k = mv² / 2 . Тогда для системы м. т. или тела . Используя связь линейной скорости с угловой в виде v_i = r_i, получим . (10)

Замечание: При плоском движении тел (например, цилиндр скатывается по наклонной плоскости) полная скорость

, (11)

где С  центр инерции.

Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс (центра инерции) и кинетической энергии вращательного движения тела относительно точки С, т. е.

. (12)

Замечание: При скатывании тела (без проскальзывания) на него действует сила трения покоя .