13. Движение частицы в потенциальном поле

Полная энергия классической частицы

W = W_o + W_k + W_p(r ), (28)

где W₀ = mc² – энергия покоя частицы; W_k = p²/ 2m – кинетическая энергия частицы; W_p(r) – потенциальная энергия во внешнем силовом поле.

Пусть энергия покоя частицы равна нулю, т. е. начало отсчета выбрано на уровне энергии покоя. Как известно, кинетическая энергия не может быть отрицательной, т. е. W_k =  0.

Cледовательно, во всех точках пространства, в которых частица может находиться в данный момент времени, потенциальная энергия меньше или равна полной энергии частицы, т. е. W_p(r)  W = const. Поэтому частица не может проникать в области пространства, где значение потенциальной энергии силового поля превосходит полную энергию частицы.

Вывод: Если полная энергия частицы меньше значения ее потенциальной энергии, то частица может проникать только в ограниченную область пространства – такое движение называют финитным.

Примером финитного движения является движение планет в Солнечной системе. Такое движение является весьма устойчивым, поскольку Солнечная система существует около пяти миллиардов лет.

Вывод: Если же частица может удаляться на неограниченное расстояние от системы отсчета, то такое движение называется инфинитным. Примером инфинитного движения является движение электрического заряда в поле одноименного заряда. Ограничения, связанные с инфинитными и финитными движениями, существуют только в классической механике. В квантовой механике возможен эффект

просачивания частиц сквозь «потенциальный барьер».

1. Пусть полная энергия частицы отрицательна (W₁< 0), тогда неравенство W_p(r)  W₁ = const.

Следовательно, частица всегда находится внутри «потенциальной ямы» – движение является финитным, кроме того, будет периодически повторяться, т. е. частица совершает колебательное периодическое движение.

W₁ = W_p(A) = mv² / 2 + W_p(A),

т. е. в точке поворота скорость частицы обращается в нуль.

Таким образом, границы движения классической частицы определяются значением полной энергии.

Например, если W = W_p2  0, то движение частицы станет инфинитным.

В потенциальном силовом поле на частицу действует возвращающая сила F_x =  dW_p/ dx , а в крайних точках на частицу действует максимальная сила.

Поэтому точке минимум потенциальной энергии, определяет положение устойчивого равновесия.

Рис. 15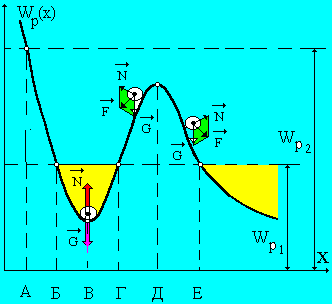

2. Пусть график функции W_p(х) «Потенциальная яма» между точками х = Б и х = Г отделена справа потенциальным барьером х = Г, х = Д и х=Е.

В связи с этим движение частицы с полной энергией внутри «потенциальная яма» между точками х = Б, х = Г будет финитным.

Если же частица выйдет за потенциальный барьер, то ее движение станет инфинитным, но уже с одной граничной точкой х = Е.

В случае, когда полная энергия частицы равна , движение частицы является инфинитным в области пространства от х = А до х  , а точкой устойчивого равновесия – т. х = В. В точке х = Д, которая является точкой неустойчивого равновесия, потенциальная энергии максимальна.

Однако при малейшем смещении частицы из точки х = Д сразу же возникает возвращающая сила, которая стремится удалить частицу в ту область пространства, где потенциальная энергия частицы будет минимальной.