6. Потенциальная энергия

Другим видом механической энергии является потенциальная энергия.

Энергию взаимного расположения тел, учитывающую вид их взаимодействия, называют потенциальной энергией.

Рис. 7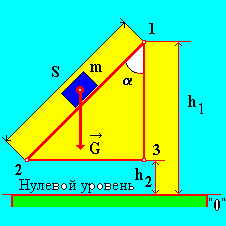

Найдем работу силы тяжести, которую она совершает при равномерном движении тела без трения из положения 1 в 2 вдоль наклонной плоскости. Длина наклонной плоскости – S.

Высота от нулевого уровня до точки 1 равна h₁, до точки 2 – h₂. Угол между вертикалью (отвесной линией) и наклонной плоскостью равен .

Работа на участке S₁₂

A₁₂ = mg cos  S,

где mgcos  – проекция силы тяжести на направление перемещения,

S cos  =h₁ – h₂,

или

A₁₂ = mg h₁ – mg h₂.

Величину W_P = mgh – называют потенциальной энергией, которой обладает тело массой m, поднятое над поверхностью Земли.

В этом случае работа силы тяжести запишется в виде

A₁₂ = W_P1 – W_P2,

где W_P1 – потенциальная энергия тела в состоянии 1; W_P2 – потенциальная энергия тела в состоянии 2.

Окончательно, A₁₂ =  (W_P2  W_P1) =  W_P. (14)

Вывод: Работа силы тяжести равна убыли потенциальной энергии со знаком минус.

7. Консервативные и диссипативные силы

Вычислим работу силы тяжести на замкнутой траектории (1231).

Полную работу на замкнутой траектории (1231) представим как сумму работ на отдельных участках пути:

А = А₁₂ + А₂₃ + А₃₁.

1. Работу силы тяжести на участке 1  2 (А₁₂) мы уже нашли:

A₁₂ = mg cos  S.

2. Работа силы тяжести на участке (2  3) равна нулю, так как угол между на правлением перемещения и направлением действия силы тяжести равен 90^о,

т. е. А₂₃ = 0. 3. Работа силы тяжести на участке (3  1)

Рис. 8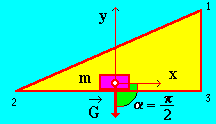

A₃₁ =  mgh,

где h = h₁  h₂ = S cos, так как угол между направлением перемещения и направлением действия силы тяжести равен 180⁰.

Вывод: Полная работа силы тяжести на замкнутом пути равна нулю.

Этот вывод может быть распространен на случай любой замкнутой траектории произвольной формы.

Силы, работа которых на замкнутом пути равна нулю, называют консервативными, или потенциальными.

Кроме того, работа консервативных сил не зависит от вида траектории перемещения тела, а зависит только от координат его начального и конечного перемещений. Примерами таких сил, кроме силы тяжести, являются силы упругости и силы электромагнитного взаимодействия. Все силы, не относящиеся к консервативным, являются не потенциальными (неконсервативными). К ним относятся диссипативные силы, например, силы трения и сопротивления.

Диссипативными называют силы, работа которых отрицательна.

К неконсервативным силам относятся также гироскопические силы Лоренца и Кориолиса. От консервативных сил они отличаются тем, что определяются не только положением, но и скоростью движения тел. Работа таких сил равна нулю.