16

Физические основы механики

Лекция 4

Законы сохранения механической энергии

2. Работа постоянной силы

Рис. 2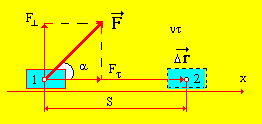

Механическая работа совершается, если тело (м.т.) под действием силы перемещается. Величина работы постоянной силы ( ) равна произведению ее составляющей F_ на направление перемещения и величины этого перемещения:

А= F_ , =S , (1)

где F_ = F cos ,.

В векторном виде работа равна скалярному произведению вектора силы и вектора перемещения

, (2)

где

.

Согласно (2) перемещение необязательно вызывается действием силы, входящей в эту формулу. Особенно это проявляется при нахождении работы сил сопротивления и трения, которые никак не способствуют перемещению тела в заданном направлении при  0, F_сопр  0, F_тр  0.

Следовательно, работа силы совершается независимо от того, под действием каких причин тело совершает перемещение. Работа, как показывает практика, может быть положительной, отрицательной и равной нулю. Для выяснения этого воспользуемся формулой работы А = F s cos.

1. Работа силы положительна (А  0), если угол  между векторами силы и перемещения острый: cos   0.

2. Работа силы отрицательна (А < 0), если угол  тупой: cos  0.

3. Работа силы равна нулю (А = 0).

При этом возможны 3 случая:

а) F = 0, если на тело не действуют силы, но оно движется равномерно и прямолинейно,

б) r = 0, тело не перемещается, несмотря на действие силы. Пусть на тело действуют какие-то другие силы;

в) сила действует перпендикулярно к перемещению: cos  = 0, т. е.  = /2. Например, сила Кориолиса, сила Лоренца всегда перпендикулярны направлению перемещения.

В СИ работа измеряется в джоулях (Дж).

3. Работа переменой силы

Для нахождения полной работы на конечном участке пути, когда на движущее тело действует переменная сила, необходимо весь путь разбить на малые участки пути (перемещения) и найти на каждом из них элементарную работу.

Любые элементарные перемещения (малые участки пути s_i) можно считать прямолинейными, в пределах их действующая сила остается постоянной, т. е.

F_i = const. На элементарном участке пути s_i совершается элементарная работа:

А_i = F s_i cos _i.

Работа на конечном участке пути

.

Для нахождения полной работы на всём участке пути перейдем к пределу, когда . Тогда

(3)

или при бесконечно малом перемещении м. т. под действием силы совершает бесконечно малую работу (ds=dl):

. (4)

Поскольку работа не является функцией состояния системы, то она не может быть представлена в виде полного дифференциала, поэтому, вместo dA, будем использовать символ А. Полная работа на участке 1 – 2

. (5)

Если на тело одновременно действуют несколько сил: , то полная работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности:

A = A₁ + A₂ +...+ A_n = . (6)

Работу можно найти графически, где она может быть представлена площадью криволинейной трапеции. В случае прямолинейного движения тела (в прямоугольных декартовых координатах), учитывая, что

где – единичные векторы осей Х, У, Z соответственно, формулу (6) можно представить в виде

=

= Fdxcos + Fdycos + Fdzcos = F_xdx + F_ydy + F_zdz,

где , ,  – углы, которые вектор силы составляет с векторами ;

F_x = Fcos; F_y = Fcos; F_z = F cos – проекции на оси координат.