25. Момент импульса материальной точки

Одной из характеристик динамики вращательного движения является вектор момента импульса.

Вектором момента импульса м. т. относительно полюса называют векторное произведение радиус-вектора и вектора импульса относительно этого же полюса.

Радиус-вектор проводится от полюса 0 до м. т. А:

. (36)

Модуль вектора момента импульса

. (37)

Направление вектора момента импульса найдем по правилу правого винта. Вектор направлен вниз. При = /2 момент импульса м. т. максимален и равен произведению модуля радиус-вектора и модуля вектора импульса или равен произведению модуля радиус-вектора, массы м. т. и модуля скорости:

М_max = mvR, где R = rsin.

_{При  = 0}^о _{момент импульса минимален и равен нулю: Мmin = 0.}

Единицей измерения момента импульса в СИ является килограмм, умноженный на метр в квадрате, деленный на секунду.

26. Момент импульса системы материальных точек

Вектор момента импульса системы м. т. (тела) относительно полюса 0 равен геометрической сумме векторов моментов импульса, действующих на каждую м. т. в отдельности относительно того же полюса 0.

или

Переходя к модулю момента импульса тела относительно полюса 0, и используя связь линейной скорости с угловой скоростью (v_i = r_i), после подстановки в последнее выражение, получаем:

L = I , (38)

где

I = mr² -

• момент инерции системы материальных точек.

Если ось симметрии совпадает с осью вращения, то

.

В случае замкнутой системы последнее выражение приобретает простой вид:

или ,

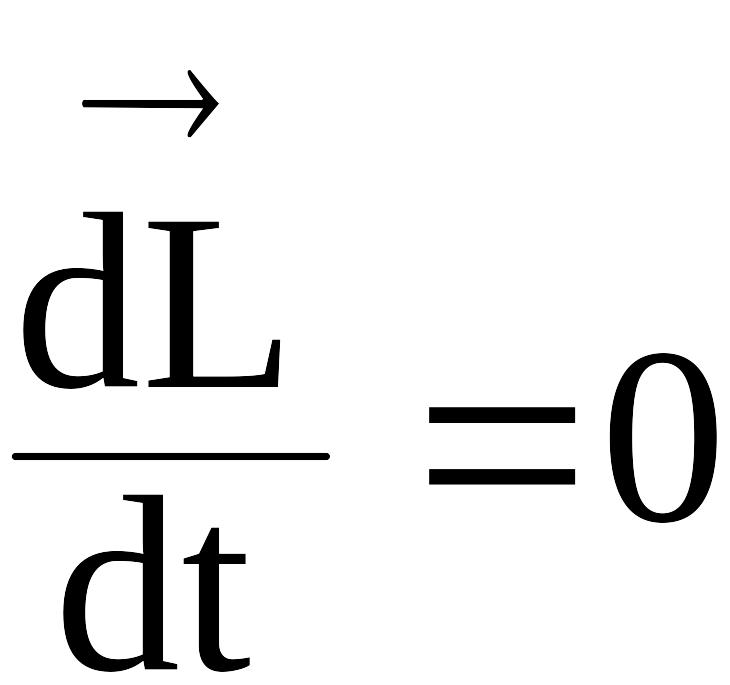т. е.

. (41)

Формула (41) выражает закон сохранения вектора момента импульса.

В замкнутой (изолированной) системе тел (м.т.) суммарный вектор момента импульса остается неизменным.

Учитывая связь момента импульса с моментом инерции, имеем

или

(42)

Закон сохранения вектора момента импульса является фундаментальным.

Замечание 1: Момент силы не зависит от того, вращается тело или нет вокруг оси, так как в состоянии покоя он уравновешен моментом других сил, действующих на это тело.

Если момент сил равен нулю, то тело вращается с постоянной угловой скоростью, т. е.

.

Если момент инерции тела не равен нулю, тогда равна нулю производная угловой скорости по времени: d / dt = 0.

Отсюда следует, что угловая скорость есть величина постоянная:

 = сonst.

Если момент инерции тела может изменяться вследствие изменения взаимного расположения отдельных его частей, то при М = 0, I = сonst.

Это значит, что изменение момента инерции тела влечет за собой изменение угловой скорости вращения, а именно: с увеличением момента инерции I его угловая скорость  уменьшается и наоборот.

Замечание 2: Закон сохранения вектора момента импульса связан с изотропностью пространства как одного из свойств симметрии пространства-времени. Под изотропностью пространства понимается следующее.

Если замкнутую систему тел повернуть в пространстве на некоторый угол (тела должны находиться в тех же условиях, что и до поворота), то это не отразится на ходе всех последующих явлений в этой системе. Используя изотропность пространства можно доказать закон сохранения вектора момента импульса. Если система замкнута, то на нее не действуют внешние силы, а действуют только внутренние. Пусть  векторы моментов внутренних сил, действующих на м.т. системы относительно неподвижного полюса 0. Затем совершим поворот всей системы вокруг полюса на малый угол d, при этом направления скоростей всех м. т. должны повернуться на такой же малый угол без изменения их величины. Вследствие изотропности пространства момент всех внутренних сил работы не совершает, т. е. А = 0 независимо от величины угла . Тогда

или .

Следовательно, .