8. Третий закон Ньютона
Из
определения силы следует, что она
является мерой взаимодействия между
телами, т. е.
(12)
или
.
(13)
Силы, с которыми взаимодействуют тела, равны по величине и противоположны по направлению. Линия действия сил лежит на одной прямой, соединяющей центры масс этих тел.
Третий закон Ньютона говорит о равенстве сил, но они приложены к различным телам, т. е. не могут иметь результирующую силу.
Третий закон Ньютона справедлив не только для двух взаимодействующих тел, но и для любого числа тел, которые взаимодействуют попарно.
На основании законов Ньютона решают прямую и обратную задачи механики:
Прямая задача: нахождение по заданным силам состояние движения тел, т. е. вычисление траектории движения.
Примером прямой задачи является вычисление скорости и траектории полета космических ракет.
Обратная задача: нахождение сил по заданному движению тела. Примером обратной задачи является открытие Ньютоном закона всемирного тяготения на основании законов движения планет Солнечной системы, полученных Кеплером.
Замечание: Часто на практике и в жизни неверно применяют термин "движение по инерции".
Например, бегун, движущийся равномерно на дистанции, запнулся за камень или другой предмет.
При этом его верхняя часть тела продолжает двигаться по «инерции», в результате он падает. Как только бегун зацепился ногой за камень, это значит, что на него подействовала сила, и в движении бегуна появилось ускорение, т. е. движение перестало быть равномерным и прямолинейным, это уже второй закон Ньютона, а не движение по инерции. Если говорить строго, то вряд ли в природе можно указать хотя бы один реальный пример движения по инерции в чистом виде.
9. Понятие сил
Третий закон Ньютона позволяет осуществить переход от механики отдельных м. т. к системе м. т. (тел).
Силы, действующие между материальными точками (телами) данной системы, называют внутренними силами (f).
Силы, действующие на тела системы со стороны других тел, не входящих в данную систему, называют внешними силами (F).
Замкнутой системой называют систему, на которую действие внешних сил компенсировано.
10. Закон сохранения вектора импульса
Используя второй закон Ньютона, запишем уравнения движения для каждой м. т.
системы с учётом внутренних и внешних сил.
где
– внутренние силы, взаимодействующих
i, j материальных точек;
–
сумма всех внешних сил, действующих на
i-ю
материальную точку системы.
Поскольку внутренние силы действуют попарно, то на основании третьего закона Ньютона сумма всех внутренних сил равна нулю.
Сложим почленно левые и правые части предыдущего выражения, получим
,
где
;
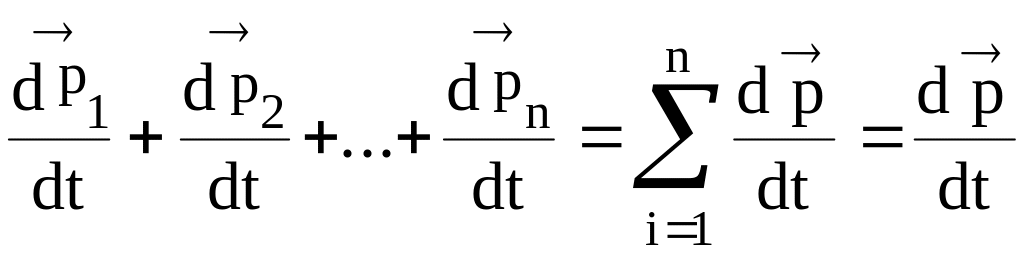(14)
–
сумма всех внешних
сил, действующих на систему.
Тогда
.
(15)
Скорость изменения вектора полного импульса системы материальных точек равна вектору результирующей внешних сил, действующих на эту систему.
Если система замкнута, то сумма всех внешних сил, действующих на эту систему, равна нулю, тогда
или
.
(16)
Формула (16) выражает закон сохранения вектора импульса.
В изолированной системе суммарный импульс м. т. (тел) системы есть величина постоянная.
Возможно изменение импульса отдельных м. т, входящих в замкнутую систему, но общий импульс системы не изменяется.
Замечание: Закон сохранения вектора импульса справедлив для замкнутых систем, но его можно применить и для незамкнутых систем, если внешние силы, действующие на систему много меньше внутренних сил и ими можно пренебречь.
Закон сохранения вектора импульса можно применять и в том случае, если нельзя пренебречь внешними силами, но проекции этих сил на какое-либо направление, например, на ось Х равны нулю, т. е.
.
Тогда рх = const.
Полный импульс системы не сохраняется, но сохраняется проекция импульса на ось Х. Например, тело движется горизонтально, вдоль оси Х.
Силами сопротивления воздуха можно пренебречь, а проекция силы тяжести на ось Х обращается в нуль, тогда проекция импульса на ось Х будет величиной постоянной.