6

Молекулярная физика и термодинамика

__________________________________________________________________________________________________________________

Лекция 16

Элементы физической кинетики

1. Понятие о физической кинетике

Микроскопическую теорию процессов, происходящих в неравновесных системах, называют физической кинетикой.

Физическая кинетика использует представления об атомно-молеку-лярном строении веществ. Поэтому ей удается вычислить кинетические коэффициенты, диэлектрическую и магнитную проницаемости (восприимчивости) и ряд других характеристик сплошных сред.

Круг вопросов, изучаемых физической кинетикой, довольно широк и многообразен, например, кинетическая теория газов, неравновесные процессы в плазме, явления переноса в жидкостях и твердых телах, кинетика фазовых переходов и др.

В классическом случае, если известна функция распределения частиц системы по импульсам и координатам в зависимости от времени (в квантовом случае – статистический оператор), то можно найти все характеристики неравновесной физической системы.

Хотя вычисление полной функции распределения затруднено, для определения, например, импульса или потока энергии достаточно знать функцию распределения ограниченного числа частиц, а для газов малой плотности – одной частицы.

Физическая кинетика позволяет получать уравнения баланса средних плотностей вещества, импульса и энергии.

При этом используют существование различных промежутков времени релаксации для неравновесных процессов, например, в газах из частиц (квазичастиц) время свободного пробега много больше времени их контакта при столкновении, что позволяет перейти от полного описания неравновесных состояний функцией распределения к описанию состояния, используя функцию распределения одной частицы по ее импульсам и координатам.

Уравнением физической кинетики является кинетическое уравнение Больцмана, как основное уравнение микроскопической теории неравновесных процессов.

Оно учитывает только парные столкновения между молекулами и справедливо при условии, что длина свободного пробега молекул значительно больше их размеров (для упругих частиц газа). Поэтому оно применимо для не слишком плотных газов.

Для решения кинетического уравнения Больцмана используют кинетическую теорию газов, которая, в свою очередь, позволяет вычислить кинетические коэффициенты и получить макроскопическое уравнение для процессов переноса, например, диффузии, вязкости и теплопроводности.

3. Диффузия в газах

Все необратимые процессы являются следствием воздействия на физическую систему внешних условий, в которых ее состояния оказываются неравновесным.

Эти явления переноса необратимы и возникают самопроизвольно в результате теплового движения при отступлении от равновесного состояния физической системы и характеризуются возникновением потоков диффузии, тепла и импульса (последний, в отличие от двух первых связан не с одним, а двумя направлениями: направлением импульса и направлением его переноса). По абсолютному значению каждый из потоков (являются вектором) равен соответственно массе вещества (диффузия), внутренней энергии (теплопроводность) и импульсу (вязкость – тензорный процесс).

Строгий молекулярно-кинетический анализ явлений переноса весьма затруднителен в виду нарушения полной хаотичности движения молекул, что приводит к отклонениям от максвелловского распределения молекул по скоростям. Рассмотрим явление диффузии в газах.

Явление взаимного проникновения и перемешивания частиц двух и более соприкасающихся физических систем называют диффузией. Если происходит перемешивание частиц одного и того же вещества, то явление называют самодиффузией. В смеси газов диффузия возникает из-за различия в концентрациях отдельных газов, составляющих смесь (рис. 2). В процессе диффузии происходит перенос массы вещества из областей с большей концентрацией в области с меньшей концентрацией. В однородном газе перенос массы вещества при диффузии описывается законом Фика, установленного опытным путем:

Рис. 2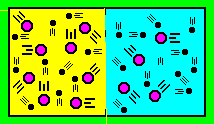

, (4)

где m – масса газа; D – коэффициент диффузии; – градиент плотности газа вдоль оси Х; S – некоторая площадка, расположенная перпендикулярно направлению переноса массы вещества; t – время переноса.

Знак «» в (4) показывает, что перенос массы вещества при диффузии происходит в направлении убывания плотности газа. В СИ коэффициент диффузии измеряется в м²/с.

Согласно молекулярно – кинетической теории коэффициент диффузии характеризует скорость переноса массы вещества и определяется по формуле

, (5)

где – средняя арифметическая скорость молекул; – средняя длина свободного пробега молекул.

В свою очередь, из молекулярно – кинетической теории известно, что

<u>  , 1/P, P  T. Следовательно, D 

Если ввести понятие вектора плотности потока диффундирующих молекул, то в общем случае трехмерной диффузии закон Фика запишется в виде:

где n₀ – концентрация молекул газа.

Закон Фика остается справедливым для диффузии в твердых телах, где диффундирующие атомы перескакивают их одного положения устойчивого равновесия в другое. Для коэффициента диффузии атомов в твердых телах справедлив закон Аррениуса

где D₀ = Ad²/ ₀, d – межатомное расстояние,

W_p – энергия активации, А – зависит от структуры кристалла, ₀ = 1/₀, ₀  10¹³ с^1 – собственная частота колебаний атома.

В жидкостях механизм диффузии более сложен, т. к. здесь одновременно проявляются элементы механизмов диффузии в газах и твердых телах.