11

Статистическая физика и термодинамика

Лекция 15

ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

1. Вероятность и флуктуации

Отличительной особенностью внутреннего движения частиц макроскопических тел является его случайный характер. Такая неопределенность характерна для микроскопического подхода к внутреннему движению большего числа частиц, составляющих тела.

В таких случаях говорят о вероятности того, что какие-либо физические величины будут иметь те или иные значения.

Термодинамическая вероятность – число способов, которыми может быть реализовано данное состояние макроскопической физической системы.

Каждое состояние физической системы с определенным распределением ее частиц по возможным классическим или квантовым состояниям называют микросостоянием.

Термодинамическая вероятность W равна числу микросостояний, реализованных в данном макросостоянии, т. е. W  1.

Вероятность дает наиболее правдоподобную оценку доли случайных событий с данным исходом при большом числе их повторений.

Наличие случайных отклонений от наиболее правдоподобного значения является причиной возникновения флуктуаций.

В теории вероятности установлено, что наиболее вероятными являются малые флуктуации.

Флуктуации физической системы, находящейся в состоянии термодинамического равновесия, всегда малы и имеют статистическую природу.

3. Распределение Больцмана

Из-за хаотического движения изменения в положении каждой частицы (молекулы, атома и т. д.) физической системы (макроскопического тела) носят характер случайного процесса.

Поэтому можно говорить о вероятности обнаружить частицу в той или иной области пространства.

Из кинематики известно, что положение частицы в пространстве характеризуется ее радиус-вектором или координатами.

Рассмотрим вероятность dW( ) обнаружить частицу в области пространства определяемой малым интервалом значений радиус-вектора

,

если физическая система находится в состоянии термодинамического равновесия.

Векторный интервал

будем измерять объемом

dV = dxdydz.

Плотность вероятности (функция вероятности распределения значений радиус-вектора )

.

Частица в данный момент времени реально где-то находится в указанном пространстве, значит должно выполняться условие нормировки

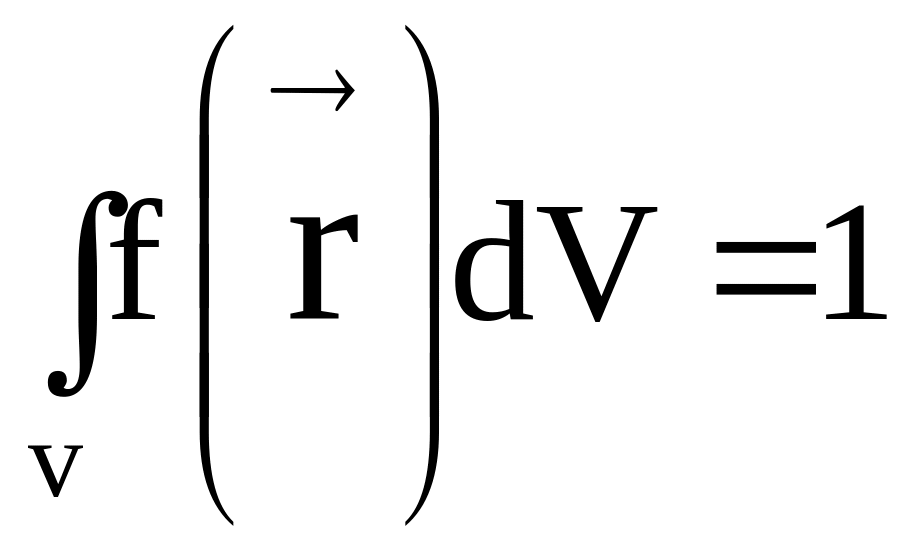
Найдем функцию вероятности распределения частиц f( ) классического идеального газа. Газ занимает весь объем V и находится в состоянии термодинамического равновесия с температурой Т.

При отсутствии внешнего силового поля все положения каждой частицы равновероятны, т. е. газ занимает весь объем с одинаковой плотностью.

Поэтому f( ) = const.

Используя условие нормировки, найдем, что

,

т. е.

f(r) = .

Если число частиц газа N, то концентрация

n = .

Следовательно,

f( ) = .

Вывод: в отсутствие внешнего силового поля вероятность dW( ) обнаружить частицу идеального газа в объеме dV не зависит от положения этого объема в пространстве, т. е.

.

Поместим идеальный газ во внешнее силовое поле.

В результате пространственного перераспределения частиц газа плотность вероятности f( )  const.

Концентрация частиц газа n и давление его Р будут различными, т. е. в пределе

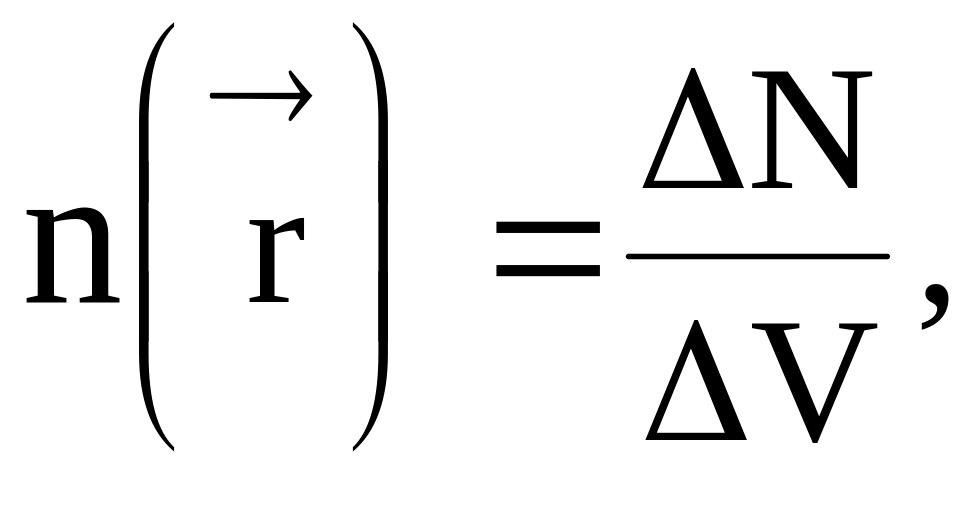
где N – среднее число частиц в объеме V и давление в пределе

,

где F – абсолютное значение средней силы, действующей нормально на площадку S.

Если силы внешнего поля являются потенциальными и действуют в одном направлении (например, сила тяжести Земли направлена вдоль оси Z), то силы давления, действующие на верхнее dS₂ и нижнее dS₁ основания объема dV, не будут равны друг другу (рис.2).

В этом случае разность сил давления dF на основания dS₁ и dS₂ должна быть скомпенсирована действием сил внешнего поля .

Рис. 2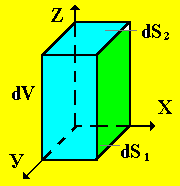

Суммарная разность сил давления

dF = nGdV,

где G – сила, действующая на одну частицу со стороны внешнего поля.

Разность сил давления (по определению давления)

dF = dPdxdy.

Следовательно,

dP = nGdz.

Из механики известно, что потенциальная энергия частицы во внешнем силовом поле связана с силой этого поля соотношением

.

Тогда разность давлений на верхнее и нижнее основания выделенного объема dP =  n dW_p.

В состоянии термодинамического равновесия физической системы ее температура Т в пределах объема dV везде одинакова. Поэтому используем уравнение состояния идеального газа для давления dP = kTdn.

Решив совместно последние два равенства получим, что

 ndW_p = kTdn

или

.

После интегрирования найдем, что

,

где – постоянная интегрирования (n₀ – концентрации частиц в том месте пространства, где W_p = 0).

После потенцирования, получим

. (11)

Вывод: В состоянии термодинамического равновесия концентрация (плотность) частиц идеального газа, находящегося во внешнем силовом поле, изменяется по закону, определяемому формулой (11), которую называют формулой Больцмана.

Поэтому функция вероятности распределения принимает вид

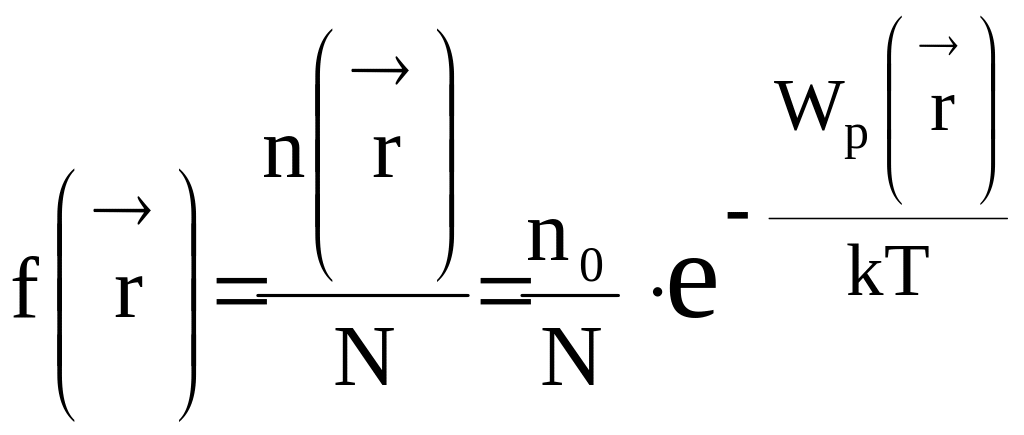. (12)

Вероятность обнаружить частицу идеального газа в объеме dV, расположенного у точки, определяемой радиус-вектором , представим в виде

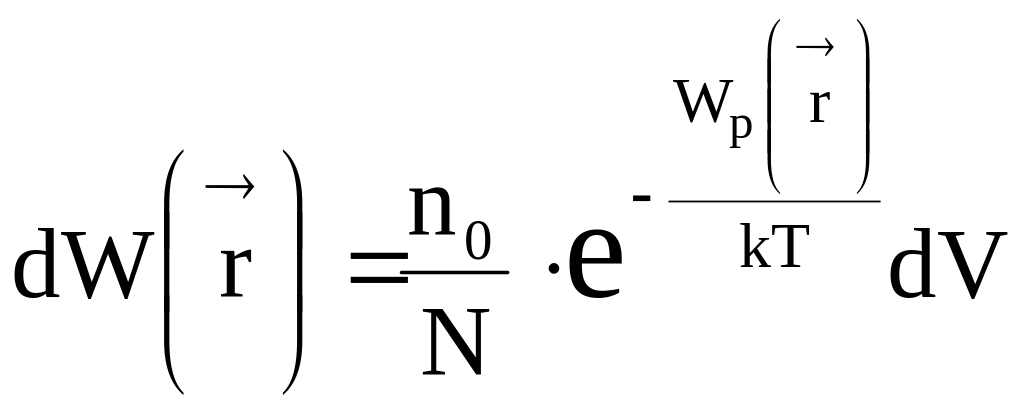. (13)

Для идеального газа давление отличается от концентрации только постоянным множителем kT, т. е.

P = nkT.

Следовательно, для таких газов давление

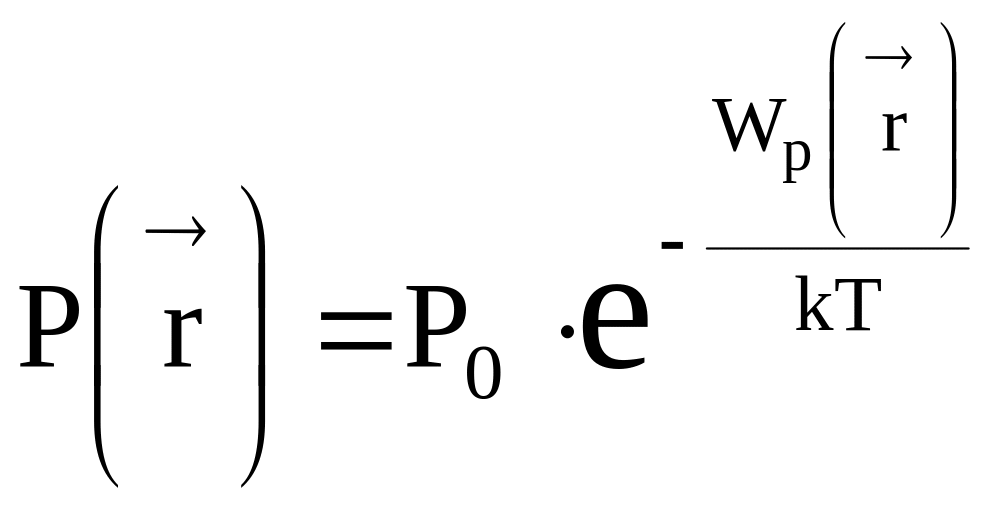, (14)

где

Р₀ = n₀kT.

Применим распределение Больцмана к атмосферному воздуху, находящему в поле тяготения Земли.

В состав атмосферы Земли входят газы:

азот – 78,1 %; кислород – 21 %; аргон – 0,9 %. Масса атмосферы – 5,1510¹⁸ кг.

На высоте 20–25 км – слой озона. Вблизи земной поверхности потенциальная энергия частиц воздуха на высоте h,

W_p= m₀gh,

где m₀ – масса частицы. Потенциальная энергия на уровне Земли равна нулю (W_p = 0).

Если в состоянии термодинамического равновесия частицы земной атмосферы имеют температуру Т, то изменение давления атмосферного воздуха с высотой происходит по закону

. (15)

Формула (15) называется барометрической формулой; применима для разреженных смесей газов.

Заключение: Для земной атмосферы, чем тяжелее газ, тем быстрее падает его давление в зависимости от высоты, т. е. по мере увеличения высоты атмосфера должна все более обогащаться легкими газами.

Из-за изменения температуры атмосфера не находится в равновесном состоянии.

Следовательно, барометрическую формулу можно применять к малым участкам, в пределах которых изменения температуры не происходит.

Кроме того, на неравновесность Земной атмосферы влияет гравитационное поле Земли, которое не может удержать ее вблизи поверхности планеты. Происходит рассеивание атмосферы и тем быстрее, чем слабее гравитационное поле.

Например, земная атмосфера рассеивается достаточно медленно. За время существования Земли ( 4–5 млрд лет) она потеряла малую часть своей атмосферы (в основном легких газов: водорода, гелия и др.).

Гравитационное поле Луны слабее земного, поэтому она практически полностью потеряла свою атмосферу. Неравновесность Земной атмосферы можно доказать следующим образом.

Допустим, что атмосфера Земли пришла в состояние термодинамического равновесия и в любой точке ее пространства она имеет постоянную температуру.

Применим формулу Больцмана (3.11), в которой роль потенциальной энергии выполняет потенциальная энергия гравитационного поля Земли, т. е.

где  – гравитационная постоянная; М_з – масса Земли; m₀ – масса частицы воздуха; r – расстояние частицы от центра Земли. При r   W_p = 0.

Поэтому формула Больцмана принимает вид

, (16)

где n_ – плотность (концентрация) Земной атмосферы при r  .

Если положить, что r = R_з, где R_з – радиус Земли, то

. (17)

Это означает, что n_  0. Но число частиц в атмосфере Земли конечно. Поэтому такое число частиц не может быть распространено по бесконечному объему.

Следовательно, Земная атмосфера не может находиться в равновесном состоянии.