При этом над системой совершается работа

А = Р₁V₁  P₂V₂. (19)

В адиабатическом процессе эта работа идет на изменение его внутренней энергии (первое начало термодинамики, Q = 0), т. е.

U₂  U₁ = Р₁V₁  P₂V₂. (20)

Следовательно,

U₁+Р₁V₁ = U₂+Р₂V₂ = Н = сonst, (21)

где Н – энтальпия.

Поэтому, зная уравнение состояния газа и выражение для энтальпии Н, можно найти Т. Для идеального газа внутренняя энергия и энтальпия зависят только от температуры.

Из формулы (21) следует равенство температур, т. е. для идеального газа Т = 0. Эффект Джоуля – Томсона считают положительным, если газ в процессе дросселирования охлаждается (Т < 0), и отрицательным, если газ нагревается (Т > 0).

Например, при перепаде давления на дросселе, равном атмосферному, измеренная разность температур для воздуха Т =  0,25 ^оС (опыт проводился при комнатной температуре).

Для водорода и углекислого газа в тех же условиях, разность температур составила, соответственно: = + 0,02 С; =  1,25 С.

В зависимости от условий протекания сквозь перегородку один и тот же газ может как нагреваться, так и охлаждаться.

Рис. 7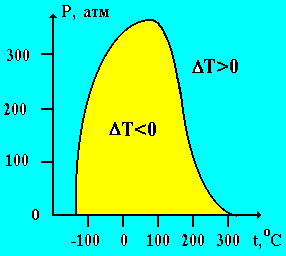

Температура Т_i, при которой разность Т, переходя через нулевое значение, меняет знак, называется температурой инверсии эффекта Джоуля – Томсона.

Совокупность точек температуры инверсии на диаграмме Р – Т называют кривой инверсии. Для точек на самой кривой эффект равен нулю.

На рис. 7 приведена кривая инверсии азота.

Из условия постоянства энтальпии следует, что эффект Джоуля – Томсона характеризуется небольшими изменениями температуры при малых перепадах давления.

Поэтому дифференциальный эффект можно описать формулой

, (22)

где – теплоемкость газа при постоянном давлении; Н – энтальпия.

Кривая инверсии реального газа соответствует уравнению

RTbV² = 2a (V – b)². (23)

Так как эффект Джоуля – Томсона является необратимым процессом, энтропия газа возрастает.

Эффект Джоуля – Томсона является одним из способов получения низких температур в комбинации с адиабатическим расширением при сжижении газов.

На практике при больших перепадах давления на дросселе температура газа может изменяться довольно значительно (интегральный эффект Джоуля – Томсона).

Например, при дросселировании от 200 атм до 1 атм и начальной температуре t = 17 ^оС воздух охлаждается на 35 ^оС.

7. Поверхностное натяжение.

Капиллярность

Любая жидкость характеризуется поверхностным слоем. Рассмотрим, почему капли дождя, капельки пролитой ртути и т. д. имеют форму, близкую к сферической? Поверхность жидкости образует пленку, и сила натяжения действует параллельно поверхности из-за существующих между молекулами жидкости сил притяжения.

Этот эффект и называют поверхностным натяжением.

Сила, действующая на единицу длины контура, ограничивающего ее поверхность, называют поверхностным натяжением.

Согласно определению, поверхностное натяжение

. (24)

Существование поверхностного натяжения можно объяснить на основании молекулярного строения вещества. Между молекулами жидкости действуют силы притяжения.

Молекула Б внутри жидкости находится в равновесии, так как силы со стороны других молекул, ее окружающих, действуют на нее во всех направлениях и взаимно компенсируются (рис. 8).

Молекула А на поверхности жидкости тоже находится в равновесии, но на нее действует результирующая сила, направленная внутрь жидкости. Эта сила и вызывает поверхностное натяжение.

При таком стягивании поверхности жидкости она стремится к состоянию, в котором площадь ее поверхности минимальна.

Рис. 8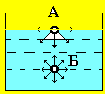

В условиях невесомости капли любой жидкости независимо от ее размеров имеют сферическую форму. Помещая каплю жидкости, например, оливкового масла, в жидкость такой же плотности (смесь спирта и воды) наблюдают, что эта капля принимает сферическую форму (опыт Плато).

Для увеличения поверхности жидкости необходимо приложить силу. Совершаемая при этом работа затрачивается на перенос молекул из глубины жидкости на ее поверхность, т. е.

А = Fx =  x = S, (25)

где x – смещение границы пленки; S – изменение площади поверхности.

При этом увеличивается потенциальная энергия молекул, называемая поверхностной энергией.

Чем больше площадь поверхности, тем больше поверхностная энергия.

Из (25) следует, что

, (26)

т. е. поверхностное натяжение – работа, совершаемая силами для увеличения площади поверхности жидкости на единицу.

а б

Рис. 9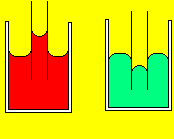

В предельном случае можно получить тонкие пленки, например, мыльные пленки, которые имеют две поверхности, между которыми заключена жидкость. При растяжении поверхности пленки увеличивается ее площадь, в остальном пленка остается такой же, так как пленка пополняется молекулами жидкости из внутренних слоев.

При определении поверхностного натяжения необходимо учитывать среду, с которой жидкость граничит. Действительно, на молекулы поверхностного слоя действуют молекулярные силы не только со стороны данной жидкости, но и со стороны молекул окружающей среды.

Если жидкость находится в сосуде, то у стенок сосуда она может подниматься или опускаться относительно общего уровня.

Это зависит от свойств жидкости и материала сосуда.

Например, вода в стеклянном сосуде около его стенок поднимается. В этом случае говорят, что вода смачивает стекло (рис. 9, а).

Наоборот поверхность ртути в стеклянном сосуде у его стенок несколько опускается, т. е. ртуть не смачивает стекло (рис. 9, б).

а б

Рис. 10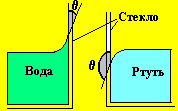

Явление смачивания (не смачивания) зависит от того, что сильнее: взаимодействие между молекулами жидкости (когезия) или взаимодействие между молекулами жидкости и молекулами материала сосуда (адгезия). У стенок сосуда жидкость образует искривленную поверхность.

Угол между касательной к поверхности жидкости и поверхностью твердого тела (стенки сосуда) называют краевым углом . Его величина зависит от соотношения сил когезии и адгезии (рис. 10, а, б). При   90^о жидкость смачивает твердое тело; при   90^о – не смачивает. Особенно четко это явление наблюдается, когда жидкость налита в узкий сосуд (капилляр). Высота поднятия (опускания) h жидкости в капилляре зависит от поверхностного натяжения, краевого угла и радиуса капилляра.

Рис. 11

Если поверхность жидкости выпукла (вогнута), то при равновесии давление по разные стороны от нее будет неодинаковым (рис. 11), т. е.

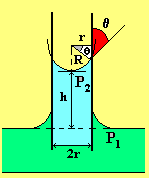
, (27)

где r – радиус капилляра; Р₁ – атмосферное давление; Р₂ – давление на уровне мениска (столба жидкости на высоте h).

Если же жидкость ограничена поверхностью двойной кривизны (мыльная пленка), то по формуле Лапласа

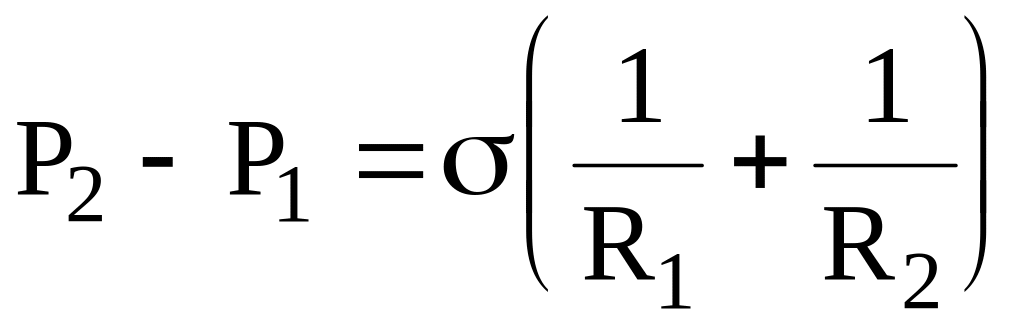, (28)

где R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости. Радиус считается положительным, если сечение вогнуто в сторону жидкости и, наоборот, если сечение выпукло, – отрицательным. В случае сферической поверхности

R₁ = R₂ = R, значит,

. (29)

Для мыльного пузыря из-за двойной поверхности натяжения

. (30)

Для жидкости в цилиндрическом сосуде из-за симметрии при

R₁ = R₂ = R – радиус кривизны (мениск)

. (31)

С другой стороны,

Р₂ – Р₁ = gh. (32)

Из формул (29), (31) и (32) можно найти высоту поднятия (опускания) столба жидкости в капилляре

. (33)

Интересен вопрос о том, каким образом вода и растворенные в ней минеральные соли поднимаются к верхушкам деревьев? Например, секвойя в своем росте достигает высоты более 100 м.

Известно, что капиллярная система деревьев (ксилеме) характеризуется радиусом капилляров от 0,01–0,3 мм.

Рис. 12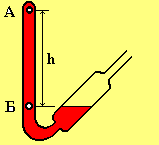

Под действием сил поверхностного натяжения вода в капиллярах поднимается на высоту не более, чем на 1,5 м. Под действием атмосферного давления она может подняться не выше 10 м. Как же осуществляется питание деревьев при их росте? Причина заключается в том, что вода поднимается за счет когезии (силы взаимодействия между молекулами однородной жидкости) и за счет отрицательного давления, которое по последним данным достигает 25 атм у верхушки деревьев. Получить на практике отрицательное давление трудно. Запаянная с верхнего конца стеклянная трубка заполняется жидкостью. Из правого резервуара откачивают воздух.

В точках А и Б возникает разность давлений (рис. 12) Р_Б – Р_А = gh.

Когда давление над жидкостью становится равной нулю, то давление в точке Б также равно нулю (Р_Б = 0), так как она находится на одном уровне с поверхностью жидкости в резервуаре.

Следовательно, давление в точке А будет иметь отрицательное значение: Р_А=  gh.

Таким способом удалось на практике получить отрицательное давление до Р =  270 атм.

При отрицательном давлении жидкость как бы стягивает на себя стенки сосуда. Возникшее натяжение существует во всем объеме жидкости, а не только на ее поверхности. Жидкость остается сплошной средой благодаря действию сил когезии между молекулами жидкости и сил адгезии между молекулами жидкости и молекулами материала стенок сосуда.

Силы когезии довольно велики. Например, прочность воды на разрыв составляет  310⁷ Н/м².