27

Элементы термодинамики

_____________________________________________________________________________

Лекция 14

1. Уравнение Ван-дер-Ваальса

Экспериментальные исследования вязкости, удельной теплоемкости и других физических свойств показали, что реальные газы по своим свойствам значительно отличаются от идеальных газов и связаны с молекулярным взаимодействием между молекулами реального газа.

Между ними существуют силы притяжения и отталкивания.

Зависимость силы взаимодействия молекул от расстояния между ними приведена на рис. 1, а.

Рис. 1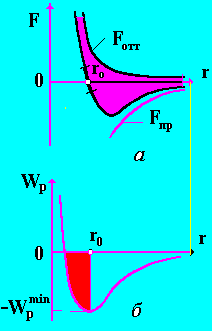

При r = r₀ силы притяжения и отталкивания равны по абсолютной величине.

Если r > r₀, то преобладают силы притяжения, особенно на больших расстояниях, что и приводит к конденсации газа в жидкость.

При r < r₀ преобладают силы отталкивания, что свидетельствует о наличии собственных размеров молекул. При взаимодействии молекулы обладают потенциальной энергией. График зависимости W_p = W_p(r) приведен на рис. 1, б.

С учетом рассмотренного выше, Ван-дер-Ваальс предложил модель реального газа и получил уравнение, описывающее его состояние. Для этого были введены поправки в уравнение состояния идеального газа, учитывающие собственный объем молекул и их взаимодействие.

Первая поправка связана с существованием ограниченной сжимаемости реального газа. Следовательно, в уравнении

(1)

нужно заменить V на V  Nb, где b = 16r³/3 – поправка на собственный объем молекул, учитывающая действие сил притяжения между молекулами; N – число молекул, r – радиус молекулы.

Тогда формула (1) принимает вид

. (2)

Вторая поправка связана с существованием притяжения между молекулами, которое приводит к уменьшению давления реального газа на стенки сосуда, так как на любую молекулу, вблизи стенок сосуда, действует со стороны остальных молекул результирующая сила, направленная внутрь сосуда и пропорциональная концентрации молекул: n₀ = . Кроме того, давление также прямо пропорционально концентрации молекул (Р = n₀kT).

Следовательно, полное давление уменьшится на величину, прямо пропорциональную квадрату концентрации газа, т. е. на величину , где а – постоянная, учитывающая особенность сил притяжения данного сорта молекул. Поэтому формула (2) запишется в виде

. (3)

Таким образом, уравнение состояния реального газа запишем в виде:

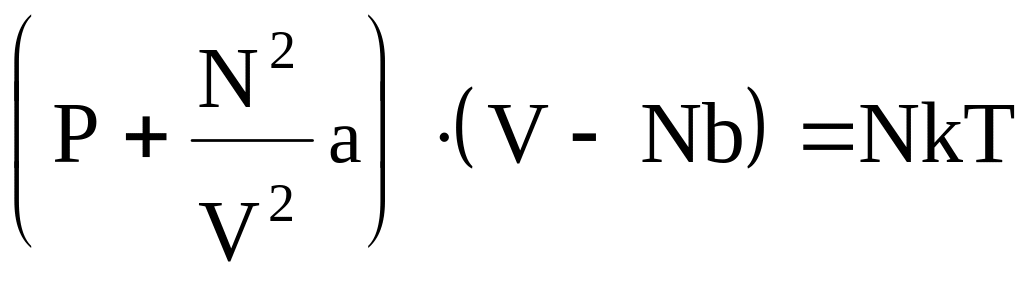(4)

или

(5)

Для одного моля реального газа уравнение состояния имеет вид:

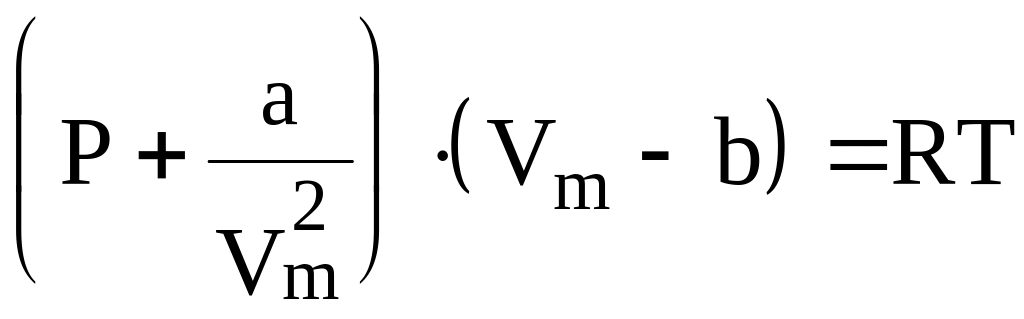. (6)

Исследуем теоретические изотермы реального газа, приведенные на диаграмме Р – V при различных значениях температуры (рис. 2).

Уравнение (5) имеет три корня, из которых вещественными корнями могут быть все три или один корень.

Физический смысл имеют только положительные корни. На кривой (изотерма Т₁) им соответствуют точки б, г, е, рис. 2. Для выяснения физического смысла различных участков теоретических изотерм реального газа рассмотрим одну из них, например, изотерму Т₁ (а – б– в – г – д – е – ж). На участках (а – б – в) и (д – е – ж) зависимость давления от объема имеет нормальный вид. Участок изотермы (в – г – д) не может быть осуществлен, так как нет в природе таких состояний, когда при сжатии вещества его давление уменьшается. Наличие этого участка изотермы показывает, что при постепенном изменении объема вещество не может быть в виде однородной массы, так как при определенном давлении и температуре наступает распад вещества на две фазы. Эксперименты показали, что изотермы реальных газов (изотермы Эндрюса), в отличие от теоретических изотерм, имеют вид кривой (а – б – г – е – ж, рис. 2), где прямолинейный участок (б – г – е) соответствует двухфазному состоянию. При повышении температуры прямолинейные участки изотерм сокращаются, и при некоторой температуре стягиваются в точку К, называемую критической (рис. 2).

Рис. 2

Существование критической точки было предсказано Д. И. Менделеевым. Если соединить между собой последовательно правые и левые концы прямолинейных участков на семействе изотерм, то получим кривую фазового равновесия жидкости и газа (пара) на диаграмме Р – V. Максимум этой кривой и есть критическая точка К. В точке К изотермы Ван-дер-Ваальса имеют как максимум, так и точку перегиба, т. е.

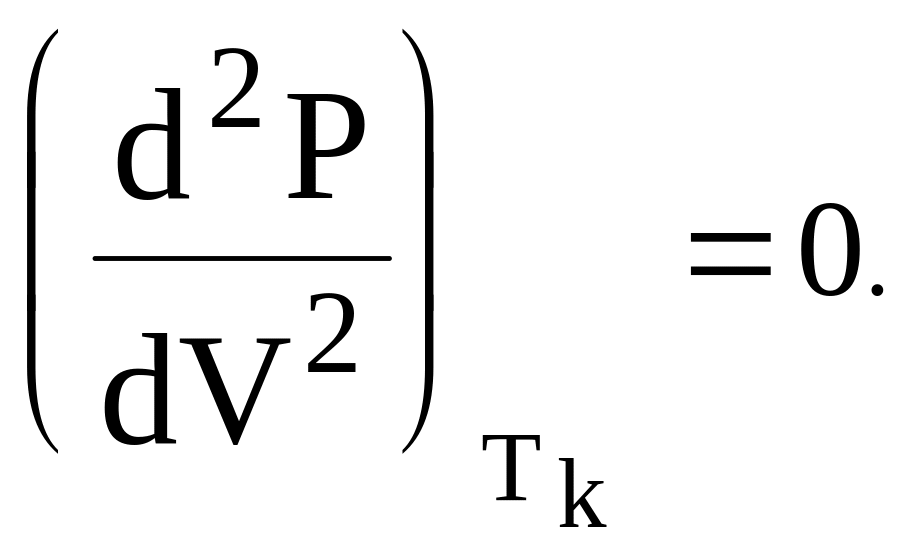
Величина, обратная первой производной, характеризует сжимаемость вещества и в критической точке обращается в бесконечность. Действительно, коэффициент сжимаемости = .

Таким образом, уравнение Ван- дер-Ваальса для реального газа не описывает существование двухфазных систем, но предсказывает существование критической точки. Уравнение Ван-дер-Ваальса выполняется только в некотором диапазоне давлений и температур, а уравнения состояния реального газа нет до сих пор. В критической точке К все три корня уравнения (4) равны V_k. Тогда формула (5), принимает вид

(7)

Это уравнение эквивалентно тождественному уравнению

(V – V_k)³ = V³ – 3V²V_k + 3VV_k² – V_k³ = 0. (8)

Из сравнения коэффициентов при одинаковых степенях объема V в уравнениях (7) и (8) получим

abN³/P_k=V_k³; 3V_k²=aN²/P_k; bN+kNT_k/P_k=3V_k. (9)

Выразим из последних равенств (.97) V_k, T_k, P_k через постоянные a, b, k и N, т. е. V_k = 3bN; P_k = a/(27b²); T_k = 8a/(27kb).

Уравнение Ван-дер-Ваальса (9) приводит к закону соответственных состояний: вид уравнения состояния, записанного в приведенных величинах, одинаков для всех веществ.

Приведенными называют отношения типа:

С учетом этого, введя удельный объем, уравнение (93) преобразуем к виду:

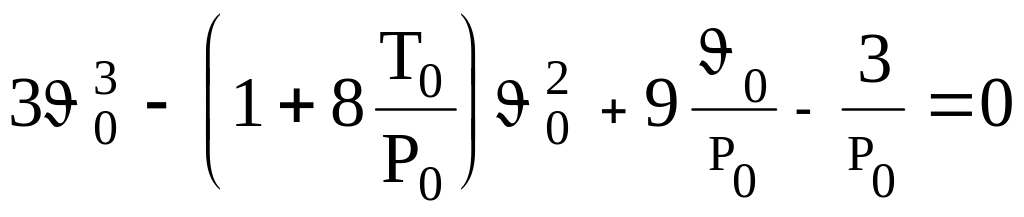
или 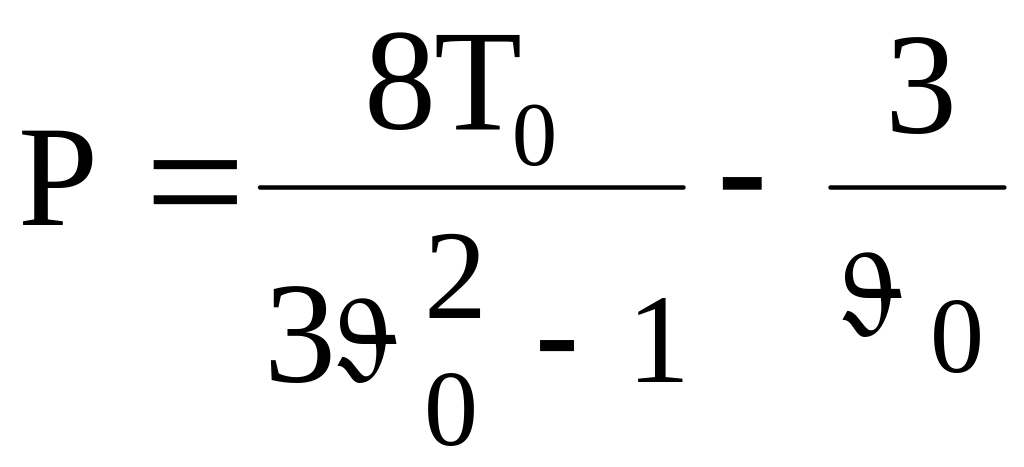. (10)

В это уравнение уже не входят постоянные а и b, характеризующие свойства реальных газов.

Рис. 3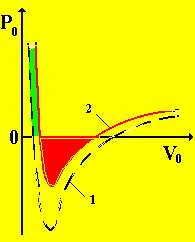

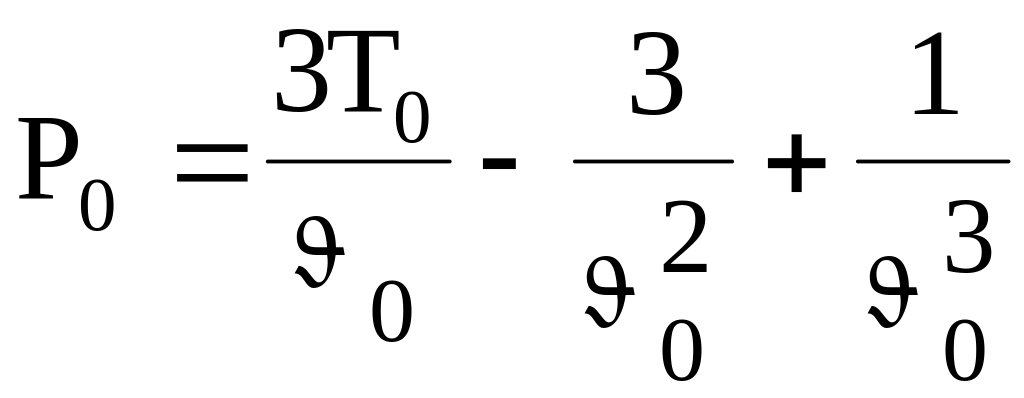Следовательно, уравнение (98) справедливо для всех газов, в том числе и для ядерного вещества, уравнение состояния которого записывают в виде

. (11)

В определенной области давлений и температур ядерное вещество ведет себя подобно молекулам реального газа под действием ядерных сил. На рис. 3 приведены изотермы, описывающие уравнение Ван-дер-Ваальса (кривая 1, рис. 3) и уравнение состояния ядерного вещества (кривая 2, рис. 3), при Т₀ = 0,5. Несмотря на различную природу, силы взаимодействия между частицами обычного и ядерного вещества, в чем-то сходны. Полученные результаты позволяют понять поведение ядерной материи в микро- и макрообъектах: при взрывах сверхновых звезд, в нейтронных звездах, черных дырах и т. д.