12. Акустический эффект Доплера

При неподвижном источнике колебаний, неподвижной среде и неподвижном приемнике частоты излучаемых, распространяемых и принимаемых волн равны.

Иначе дело обстоит, если они приходят в движение, т. е. происходит изменение частоты регистрируемых волн.

Изменение частоты колебания волн вследствие движения источника колебаний и приемника называют эффектом Доплера.

Рассмотрим несколько частных случаев, когда движется источник (приближается  удаляется), или приемник (приближается  удаляется), или оба вместе (приближаются  удаляются).

1. Источник неподвижен, приемник приближается со скоростью u₁ по прямой, совпадающей с осью Х (рис. 11, u₁ < v).

Длина волны в среде постоянна:  = ₀= v / ₀, где ₀  частота колебаний источника; ₀  длина волны в среде при неподвижном источнике.

Рис. 11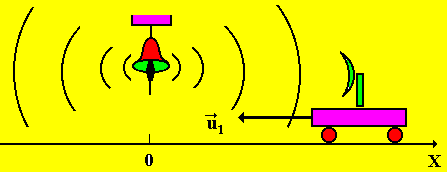

Скорость распространения волны относительно приемника

u_отн = u₁ + v,

где v  фазовая скорость волны в среде.

Тогда частота волны, регистрируемая движущимся приемником,

 = (u₁+v)/_о

или

 = _o (1 u₁/v). (54)

Знак “  " пишут в формуле (54), когда приемник удаляется.

Если приемник приближается к источнику так, что вектор его скорости образует угол ₁ с осью Х, тогда частота волны, регистрируемая приемником, определяется формулой

 = ₀ (1  u₁ сos ₁ / v). (55)

2. Приемник неподвижен, источник колебаний удаляется со скоростью u₂ вдоль оси Х (рис. 12, u₂ < v).

Рис. 12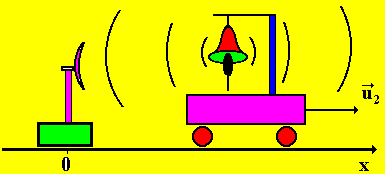

Источник удаляется в среде за время, равное периоду ( t = T₀), на расстояние u₂ T₀ = u₂ / ,

T₀ = 1/ ₀,

где ₀ и T₀  частота и период колебаний источника соответственно.

Поэтому при удалении источника длина волны в среде  отличается от длины волны при неподвижном источнике ₀ (она растет) и определяется выражением

 = ₀ + u₂T₀ = (u₂ + v) / _0, (56)

Найдем частоту, которую регистрирует приемник:

, (57)

где «  » соответствует приближению источника.

В случае, если источник движется со скоростью u₂ под углом ₂ к оси Х,

(58)

3. Общий случай

Источник и приемник движутся одновременно относительно среды со скоростями u₂ и u₁, соответственно.

В этом случае частота находится по общей формуле

(59)

Замечание: Верхний знак в формуле (59) соответствует приближению источника и приемника; нижний знак обозначает, что источник и приемник удаляются.

Читателю предлагается вывести формулу (59) самостоятельно для случая, когда приближается источник и удаляется приемник.

Вывод: Движение источника звуковых колебаний и приемника приводят к изменению частоты волны, регистрируемой приемником.

Отличие результатов объясняется различными условиями при движении приемника и источника.

Это особенно заметно, когда скорости перемещения источника и приемника близки к скорости распространения волн в среде, в том числе и звуковых.

Например, когда скорость приближения приемника к источнику составляет девять десятых от скорости распространения волн в среде (u₁= 0,9v), то частота звука, регистрируемая приемником, равна  = 10₀, а при удалении приемника  всего

 = 2₀.

Замечание: Казалось бы, какая разница что движется  источник или приемник?

Но все дело в том, что важно не относительное движение источника и приемника, а их движение относительно среды, с которой связана система отсчета, и это не противоречит принципу относительности.

Заключение. Эффект Доплера наблюдается в любой среде. Большое значение он имеет в оптике («красное смещение» или «фиолетовое»).

Эффект Доплера используется для измерения скорости движущихся объектов.

Например, при наблюдении за светящимися источниками (звезды, галактики, квазары и т. п.) в космическом пространстве наблюдается смещение спектральных линий в область красных частот, что свидетельствует об их удалении, т.е. Вселенная расширяется.