9. Дифракция механических волн

Явление огибания волнами препятствий, сравнимых с длиной волны, называется дифракцией.

При распространении волн в среде упругие колебания передаются на большие расстояния от одних частиц к другим, и это происходит не мгновенно, а с некоторой скоростью.

Для объяснения дифракции волн применяют принцип Гюйгенса.

Рис. 7

Каждая точка фронта волны, до которой распространилось волновое возбуждение, сама является источником вторичных волн.

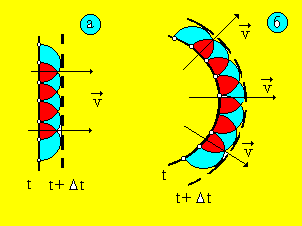
Принцип Гюйгенса позволяет в любой момент времени найти новый фронт волны как огибающую вторичных волн (рис. 7, а - плоские волны, рис. 7, б - сферические волны).

Принцип Гюйгенса используется для объяснения явления дифракции волн любой природы.

Это значит, что при распространении волн в неоднородной среде происходит отклонение их от прямолинейного распространения. Принцип Гюйгенса применим к однородным и неоднородным средам. Способность волн огибать препятствия и переносить энергию в области, лежащие за препятствием, отличает их от частиц вещества, тоже переносящих энергию.

Рис. 8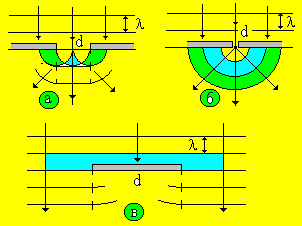

Однако это различие весьма существенно и значительно помогло объяснению дифракции света. При дифракции происходит проникновение волны в область геометрической тени (рис. 8, а- d>; б - d< ; в - d >> ). Расчет дифракционной картины связан со значительными математическими трудностями.

Хорошее качественное и количественное объяснение дифракции дает метод зон Френеля (d>), основанный на принципе Гюйгенса-Френеля.

Более подробно явление дифракции целесообразно рассматривать в разделе “Волновая оптика” на примере дифракции света.

10. Отражение и преломление волн

Большой практический и теоретический интерес представляет вопрос о распространении волн при переходе их из одной среды в другую, например, воздух - вода, вода - твердое тело и т.д.

При падении волны на границу раздела двух сред необходимо рассматривать совместно уравнения трех волн:

, (41)

где s₁ - падающая волна; s₂ - преломленная волна; s₃ - отраженная волна.

Появление в отраженной волне начальной фазы _о объясняется тем, что при отражении фаза волны может измениться.

При этом возможны два случая: 1)  = 0, 2)  = .

Поэтому формулу для отраженной волны можно переписать:

,

где “+” - соответствует отражению волны без изменения фазы, ““ - отражению волны с изменением фазы.

На границе раздела двух сред должно выполняться условие непрерывности для любой точки границы раздела: s₁ + s₃ = s_2.

Для падающей и отраженной волн волновые числа равны, т.е.

,

где v₁ - скорость распространения волны в первой среде.

Рис. 9

Используя принцип Гюйгенса, можно доказать закон отражения (рис. 9 ).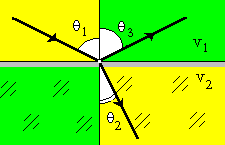

Лучи, падающий и отраженный вместе с перпендикуляром к границе раздела двух сред, лежат в одной плоскости.

Угол падения равен углу отражения:

 ₁ =  ₃ . (42)

Поскольку при переходе волны через границу раздела сред частота остается неизменной (частота вынужденных колебаний частиц второй среды равна частоте падающей волны), то волновые числа первой и второй сред будут зависеть от скорости распространения волн в этих средах:

, .

Используя принцип Гюйгенса, можно доказать закон преломления.

Предлагаем читателю самостоятельно доказать его.

Падающий луч и преломленный лежат в одной плоскости вместе с перпендикуляром к границе раздела двух сред.

Отношение синуса угла падения к синусу угла преломления равно отношению скорости распространения волны в первой среде к скорости распространения волны во второй среде:

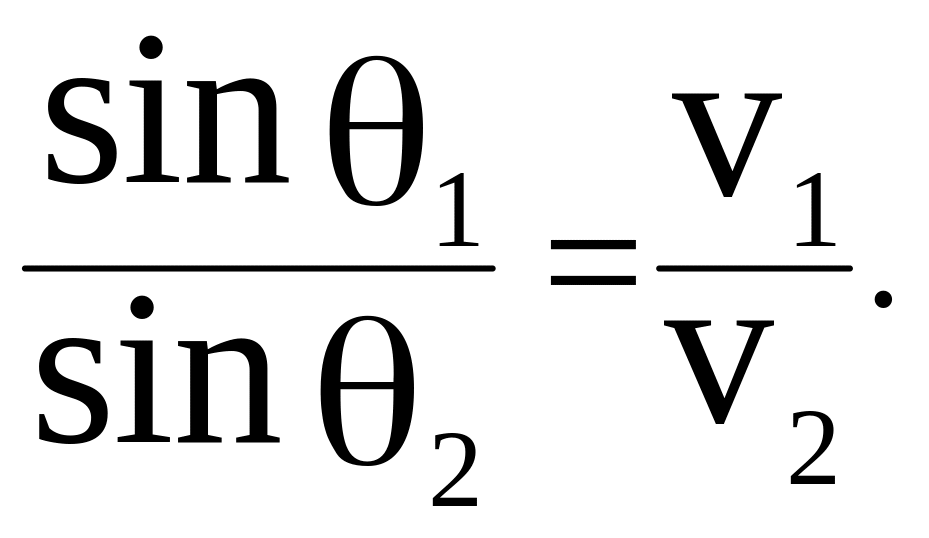
(43)

Если волна падает перпендикулярно границе раздела двух сред, то, учитывая условие непрерывности и что ₁=0, а ₂ = , получим А₁ А₃= А₂, где знак “+” соответствует отражению волны без изменения фазы; знак ““ - изменению фазы на противоположную.

Согласно закону сохранения энергии соотношение между интенсивностями всех трех волн запишется в виде

J₁  J₃ = J₂.

При отражении волны от среды с меньшим волновым сопротивлением (z=v) фаза волны не изменяется, а при отражении от среды с большим волновым сопротивлением фаза изменяется на противоположную фазу.

При прохождении волны через границу раздела двух сред используют также коэффициенты отражения R и прозрачности Т:

R =J₃/J₁, (44)

T =J₂/J₁. (45)