
- •1. Уравнение плоской бегущей волны
- •2. Волновое уравнение
- •3. Фазовая скорость
- •4. Групповая скорость
- •5. Связь фазовой и групповой скоростей
- •6. Энергия волн
- •7. Поток энергии. Вектор Умова
- •8. Интерференция волн
- •9. Дифракция механических волн
- •10. Отражение и преломление волн
- •11. Стоячие волны
- •Условие максимума.
- •2. Условие минимума
- •Собственные (резонансные) частоты стоячих волн.
- •12. Акустический эффект Доплера
- •3. Общий случай
- •13. Ударные волны
- •14. Солитоны
8. Интерференция волн
Рассматривая волновые процессы в веществах, мы использовали только уравнение одной волны. Однако на практике и в реальных средах могут распространяться одновременно несколько волн.
В результате сложения волн наблюдается ряд интересных явлений: интерференция, дифракция, отражение и преломление волн и т.д.
Эти волновые явления характерны не только для механических волн, но и электрических, магнитных, световых и т.д. Волновые свойства проявляют и все элементарные частицы, что было доказано квантовой механикой. Одно из интереснейших волновых явлений, которое наблюдается при распространении в среде двух и более волн, получило название интерференции.
Явление наложения двух и более когерентных волн, в результате которого наблюдается чередование максимумов и минимумов, называют интерференцией.
Если через произвольную точку пространства одновременно распространяются несколько волн, то это вызывает колебание частиц среды, в результате которого происходит сложение колебаний.
Если возбуждаются колебания малых амплитуд, то при наложении волн удовлетворяется принцип суперпозиции (установлен Леонардо да Винчи).
Рассмотрим процесс сложения двух волн, которые описываются следующими уравнениями:
![]() .
(27)
.
(27)
Рис. 5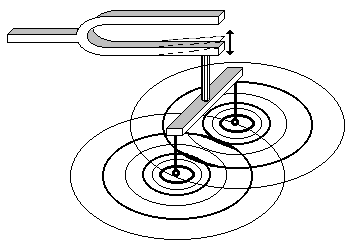
Рис. 6
На практике механические когерентные волны в среде можно получить, например, с помощью вибратора в кювете с водой (рис. 5), когда два металлических шарика, прикрепленные к одной из ножек камертона при его колебании одновременно периодически погружаются в воду, возбуждая монохроматические когерентные волны одинаковой амплитуды, частоты
и постоянной разности фаз, что и приводит к интерференции волн (рис. 6).
Найдем разность фаз складываемых колебаний при интерференции:
![]() .
(28)
.
(28)
Запишем уравнение результирующей волны в виде
![]()
После преобразований получим
 (29)
(29)
где первый сомножитель является амплитудой результирующей волны,
или
 .
(30)
.
(30)
Вывод: Результирующая волна является синусоидальной с тем же периодом Т=2/.
Рассмотрим более подробно роль результирующей амплитуды.
Условие максимума.
Разность фаз складываемых колебаний равна четному числу , т.е.
= 2m , (31)
где m = 0, 1, 2, ... называют порядком интерференции.
В равенствах (28) и (31) левые части равны, следовательно, равны и правые, т.е.
k ( x2 x1) +( o2 o1) = 2 m .
Обозначим разность x2 x1 через , т.е. = x2 x1, которую называют разностью хода волн от когерентных источников до некоторой точки пространства.
После
подстановки
![]() .
.
Если разность хода складываемых волн равна четному числу полуволн, Если положить, что o2 = o1 = 0, то мах = m = 2 m(/2). (32)
то возникает максимум: амплитуда результирующей волны удваивается (гребень волны).
Действительно,
![]() .
(33)
.
(33)
при любом значении m или
Арез= А1+А2, (34)
если А1 A2.
Вывод: Во всех точках пространства, расстояния до которых от когерентных источников отличаются на четное число полуволн, амплитуда максимальна.
Геометрическое место точек, разность расстояний от которых до источников - величина постоянная, называют гиперболой (кривая x2 x1 = сonst).
2. Условие минимума
Разность фаз складываемых колебаний равна нечетному числу :
= (2m+1) . (35)
Из (28) и (35) получим условие минимума
min
=
(2m+1)![]() .
(36)
.
(36)
Если разность хода складываемых волн равна нечетному числу полуволн, то возникает минимум:
![]() при
любом m
при
любом m
или Арез=A1 A2, (37)
если А1 A2.
Вывод: В точках пространства, расстояния до которых от когерентных источников отличаются на нечетное число полуволн, амплитуда минимальна или равна нулю.
Геометрическое место таких точек также образует гиперболу.
Гиперболы соответствующие минимуму интерференции лежат между гиперболами максимумов интерференции.
Фокусы гипербол совпадают с когерентными источниками волн.
Замечание:
1. Если складываемые волны не когерентны (1 2), то колебание будет негармоническим.
В этом случае среднее значение квадрата амплитуды результирующей волны равно сумме квадратов амплитуд складываемых волн:
![]() .
.
Результирующая фаза за период изменяется на 2.
2. Совсем другая картина наблюдается при сложении когерентных волн.
Среднее значение квадрата амплитуды результирующей волны равно квадрату суммы складываемых амплитуд, т.е.
![]() .
.
Это значит, что во втором случае величина результирующей амплитуды больше, чем в первом, на 2А1А2.
Согласно (26) интенсивность результирующей волны
 .
.
Если положить, что начальные фазы складываемых колебаний равны нулю, то
![]() (38)
(38)
где
= х2-х1;
мах
=
2m![]() .
.
Но, т. к.
cos2 m = 1
при любом m, то
![]() .
(39)
.
(39)
Соответственно для условия минимума получим, что
Jvin= 0. (40)
Замечание: Интерференция многих волн (более двух) при сложении приводит к более четкой интерференционной картине из-за возрастания амплитуды и интенсивности результирующей волны.
