5. Связь фазовой и групповой скоростей

Известно, что волновое число

или  = kv_ф.

Найдем производную по k:

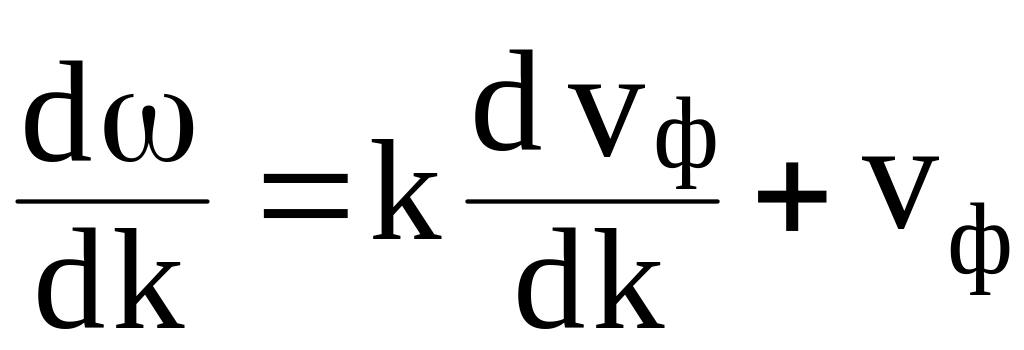. (15)

С другой стороны, волновое число можно выразить через длины волны k = .

От этого равенства возьмем производную по :

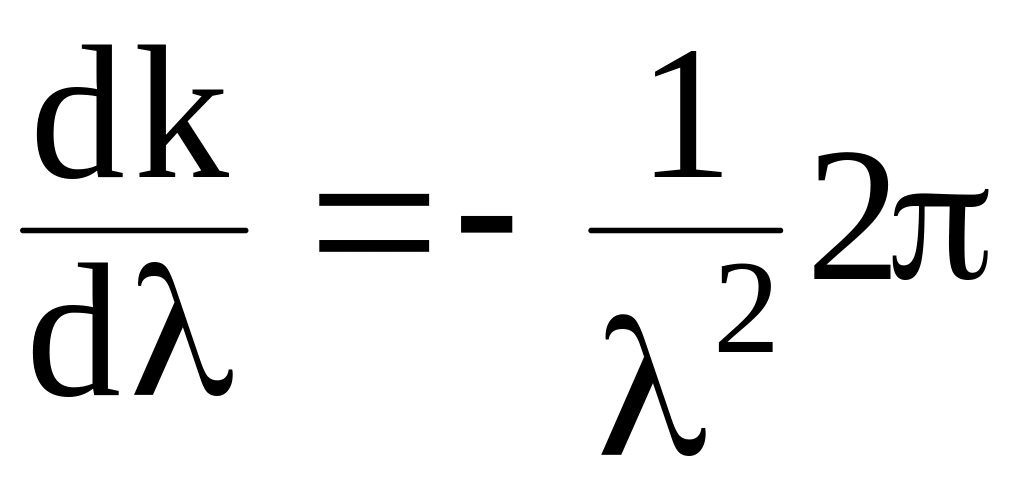
или

dk =( ) d. (16)

Выражения (15) и (16) подставим в (14).

Учитывая, что k = , получим связь фазовой и групповой скоростей:

Рис. 3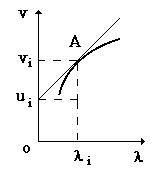

u_г = v_ф   ( ). (17)

Если в среде не наблюдается дисперсия волн, то

= 0,

тогда фазовая и групповая скорости совпадают, т. е. u_г = v_ф.

Зная зависимость скорости распространения от длины волны в среде v=f() и построив график, можно найти величину групповой скорости.

Действительно, проведя касательную к кривой в т. А (рис. 3) с координатами v_i и _i, можно найти отрезок, отсекаемый касательной на оси ординат, равный значению групповой скорости u_i (метод Эренфеста).

6. Энергия волн

При распространении волн в среде происходит перенос энергии волной. В это время в среде наблюдаются колебания ее частиц, т. е. частицы среды приобретают кинетическую (за счет движения) и потенциальную (за счет деформаций) энергии.

Найдем объемную плотность кинетической энергии w_k cреды, в которой распространяется волна:

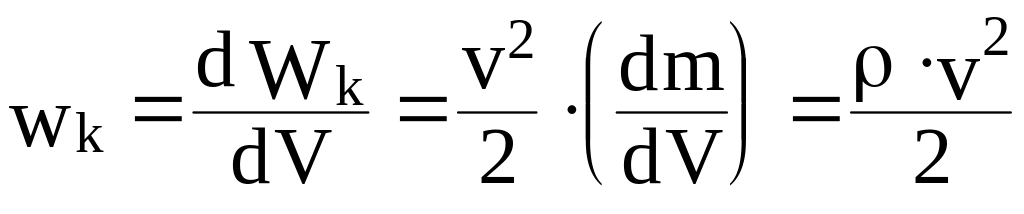, (18)

где   плотность среды;

v  скорость колебания частиц cреды.

Скорость постоянна (v = сonst) в пределах объема dV.

Запишем формулу объемной плотности потенциальной энергии cреды:

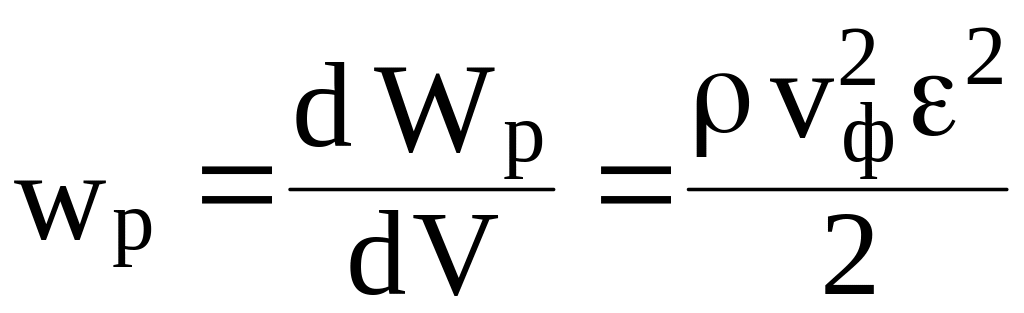, (19)

где   плотность среды; v_ф  фазовая скорость волны в среде;   относительная деформация.

Полная объемная плотность механической энергии волн в среде равна сумме объемных плотностей кинетической и потенциальной энергий, т. е.

. (20)

При распространении волн в среде непрерывно происходит передача энергии все новым и новым участкам среды за счет энергии источника.

В связи с этим объемная плотность полной механической энергии волн зависит и от координат, и от времени.

Объемная плотность полной энергии волн за период

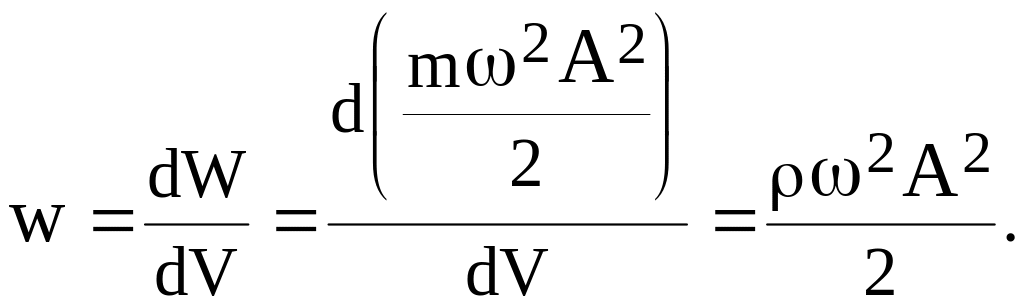(21)

7. Поток энергии. Вектор Умова

Если на пути распространения волны поставить некоторую площадку dS, то в этом случае говорят о потоке энергии через эту площадку.

Отношение энергии, переносимой сквозь некоторую площадку к промежутку времени, за который произошел ее перенос, называют потоком энергии.

Согласно определению можно записать формулу потока энергии:

dФ_э= . (22)

Используя объемную плотность энергии w, запишем полную энергию волны

dW= w (vdt) dS сos ,

где = vdt  расстояние, на которое перемещается волна, имея скорость v за малое время dt;   угол между векторами скорости и нормалью к площадке (рис. 4) или

Рис. 4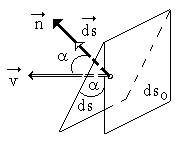

, где .

Следовательно, поток энергии переносимый волной

(23)

или

(24)

где

(25)

называют вектором Умова, или вектором плотности потока энергии.

Вывод: Модуль вектора Умова характеризует плотность потока энергии волны, переносимой через площадку перпендикулярно направлению распространению волны, т. е., U = .

Мощность потока энергии волны характеризуют интенсивностью волны.

Модуль среднего значения вектора плотности потока энергии волн, называют интенсивностью J .

Интенсивность волны  энергия, переносимая волной через единицу поверхности за единицу времени перпендикулярно к направлению распространению волны.

Для плоской бегущей и сферической синусоидальных волн за период интенсивность волны определяется выражением

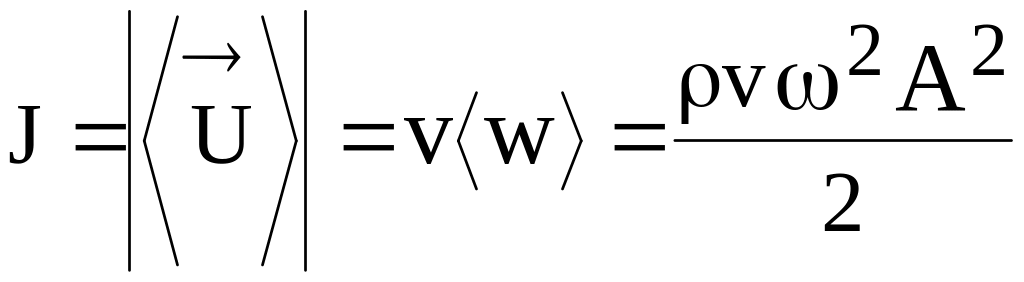. (26)

Реальные среды, в которых распространяются волны, всегда поглощают энергию. При этом происходит уменьшение амплитуды и интенсивности волны, т. е. волны затухают.