5. Фазовые переходы I и II рода

Существуют фазовые переходы первого и второго рода.

Фазовый переход I рода

Фазовым переходом первого рода называют процесс, при котором скачком изменяются внутренняя энергия, плотность, энтропия и другие свойства физической системы.

Процесс перехода I рода сопровождается поглощением или выделением тепла (теплота фазового перехода).

Примерами фазового перехода I рода являются:

1. Изменения агрегатного состояния вещества: превращение жидкости в газ (испарение) и обратный процесс превращение газа в жидкость (конденсация).

2. Переход вещества из твердого состояния в жидкое (плавление) и обратный переход из жидкого в твердое состояние (кристаллизация).

3. Превращение твердого тела непосредственно в газ (сублимация или возгонка).

Например, для превращения 1 кг воды в пар нужна энергия Q = 2,310⁶ Дж. Эта энергия необходима для преодоления сил притяжения, действующих между молекулами воды. Полиморфные превращения из одной кристаллической модификации в другую также относятся к фазовым переходам I рода, например, полиморфное превращение алмаза в графит и обратно.

Фазовый переход II рода

Фазовым переходом второго рода называют процесс, при котором скачком изменяется зависимость свойств вещества от температуры и давления.

При фазовых переходах второго рода энтропия, плотность, внутренняя энергия скачка не испытывают.

Поэтому фазовые превращения II рода не сопровождаются поглощением или выделением тепла.

К фазовым переходам II рода относят:

1. Переход жидкого гелия в сверхтекучее состояние.

2. Переход некоторых металлов и сплавов из нормального состояния в сверхпроводящее состояние.

3. Переход магнитного вещества из ферромагнитного состояния в парамагнитное состояние при нагревании магнетика до определенной температуры, называемой точкой Кюри.

2. Распределение Максвелла

В состоянии термодинамического равновесия частицы физической системы движутся в основном со скоростями, близкими к скорости их теплового движения.

Все частицы перемещаются с различными скоростями, движение которых подчиняется законам классической физики.

Найдем функцию вероятности распределения молекул идеального газа по скоростям.

Задача заключается в том, чтобы найти вероятность dW(v) обнаружения частицы, значение скорости которой заключено в интервале (v; v + dv).

Мерой интервала является малый объем

dV = dv_x dv_y dv_z

в пространстве скоростей (v – пространство), в котором по координатным осям откладываются проекции скорости v_x, v_y, v_z.

Следовательно,

dW(v) = f(v) dv, (1)

где f(v) – плотность вероятности, или функция вероятности распределения молекул по скоростям.

В связи с тем, что в данный момент времени любая молекула имеет вполне определенное значение скорости, то должно выполняться условие нормировки, т. е.

.

Функция вероятности распределения молекул по скоростям

, (2)

где k – постоянная Больцмана; m₀ – масса одной молекулы; е – основание натуральных логарифмов (е = 2,72).

Полученный результат справедлив не только для газа, но и любого тела, находящего в состоянии термодинамического равновесия, если движение его частиц подчиняется классическим законам, т. е. вид распределения не зависит от того, как взаимодействуют частицы между собой.

Определяющим фактором здесь является способность частиц обмениваться энергией при переходе к равновесному состоянию.

Следовательно, вероятность обнаружить частицу с некоторой скоростью в пределах интервала (v; v + dv), описывается функцией

. (3)

Формула (3) выражает распределение Максвелла для скоростей молекул.

Его справедливость ограничена областью применения законов классической физики для теплового движения.

Согласно (2), функция вероятности распределения зависит только от величины скорости. В рассматриваемой системе координат (v – пространство) интервал (v; v + dv) можно изобразить в виде сферического слоя (внутренний радиус сферического слоя – v, внешний – dv).

По предположению, толщина слоя интервала (v; v + dv) – мала.

Поэтому при суммировании вероятностей dW(v) в пределах сферического слоя функция распределения остается неизменной.

Тогда суммарный объем всех элементарных объемов сферического слоя V = 4v²dv.

Вывод: Для тел, находящихся в состоянии термодинамического равновесия, вероятность dW(v) обнаружить частицу этого тела со скоростью движения, абсолютное значение которой заключено в интервале (v; v + dv),

. (.4)

Полученную формулу называют распределением Максвелла по абсолютным значениям скоростей, плотность вероятности, которой

(v) = 4v²f(v) =

имеет вид

, (5)

где dW(v) = (v)dv =

– вероятность того, что модуль скорости молекулы заключен в интервале (v; v + dv).

Рис. 1

График зависимости (v) приведен на рис. 1.

Величину скорости, при которой функция (v) максимальна, называют наиболее вероятной скоростью v_в. Дифференцируя выражение (5) по аргументу v² и приравняв его нулю, получим

.

Из последнего выражения следует, что наиболее вероятная скорость

. (6)

Максимум кривой на рис. соответствует значению наиболее вероятной скорости v_в.

Из формулы (6) следует, что при увеличении температуры идеального газа (или уменьшении массы молекулы) максимум кривой смещается вправо и становится ниже при неизменной площади под кривой, а доля молекул, имеющие малые скорости, уменьшается, напротив – доля молекул с большими скоростями увеличивается.

Средняя арифметическая скорость молекул

или .

Интегрируя последнее выражение с учетом (5), получаем

. (7)

Средняя квадратичная скорость – квадратный корень из среднего значения квадрата тепловой скорости поступательного движения молекулы <v_кв> = , где .

Давление, производимое молекулами при их тепловом хаотическом движении на стенки сосуда, в котором они находятся,

или , где  = nm₀.

При постоянной температуре газа, применяя уравнение состояния идеального газа в виде

или ,

получаем

. (8)

Средняя квадратичная скорость не имеет смысла для одной молекулы, а характеризует движение всей совокупности молекул.

При t = 0 ^оC cредняя квадратичная скорость:

для азота – <v_кв> = 493 м/c;

для водорода – <v_кв> = 1838 м/c;

для кислорода – <v_кв> = 461 м/c.

Замечание: Средняя квадратичная скорость такого же порядка, что и скорость звука в газе, так как передача возмущений в звуковой волне осуществляется молекулами, движущимися с тепловыми скоростями.

Это же относится и к скорости истечения газа в вакуум.

Таким образом, все три скорости <v>, <v_кв> и v_в характеризуют тепловое движение молекул газа и различаются только числовыми коэффициентами

(9)

Изучение вероятности распределения теплового движения молекул по скоростям (распределение Максвелла) осуществлялось различными экспериментальными методами (опыты Штерна, Ламмерта и др.).

Для проведения эксперимента молекулярные пучки получают выпусканием в вакуумную камеру пучка молекул или атомов, исследуемого вещества, испаряющихся с нагревателя специальной печи.

При исследовании молекулярных (атомных) пучков используют физическое явление – эффузию газов: медленное истечение газов через малые отверстия.

От распределения молекул идеального газа по скоростям (распределение Максвелла) можно перейти к вероятности распределения молекул по значениям их кинетической энергии, т. е.

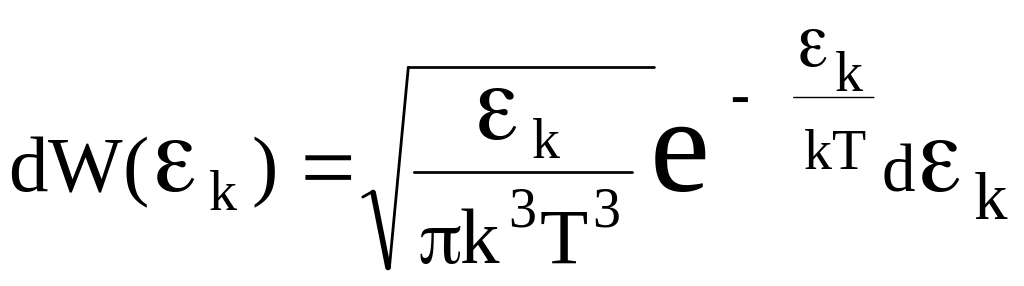. (10)

Формула (13.10) выражает вероятность dW(_к) обнаружить частицу со значением кинетической энергии из интервала (_к; _к + d_к).