Поскольку состояния 2 и 3 лежат на одной адиабате, то

,

где  – показатель адиабаты.

Состояния 1 и 4 лежат также на одной адиабате сжатия, тогда

.

Из последних равенств получаем, что

. (53^*)

После подстановки формул (2.51), (2.52) в формулу (2.50) имеем

.

Используя условие (53^*) окончательно получаем

, (53)

где  – КПД идеальной тепловой машины, работающей по прямому обратимому циклу Карно. Формула (53) выражает первую теорему Карно:

Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника; не зависит от устройства машины и вида рабочего тела.

Для реальной тепловой машины (согласно второй теореме Карно):

Коэффициент полезного действия всякой тепловой машины, работающей по циклу Карно с теми же температурами нагревателя и холодильника, что и идеальная тепловая машина, не может превосходить КПД идеальной машины, т. е. КПД находится по формуле (50).

По прямому циклу Карно работают двигатели внутреннего сгорания.

Рассмотрим обратный цикл Карно.

Работа газа за цикл

А = (Q₁  Q₂)  0,

где Q₁  0 – теплота, отводимая от холодильника; Q₂  0 – теплота, подводимая к газу при Т₂  Т₁.

Передача тепла от холодного тела к горячему происходит за счет работы внешних сил. КПД идеальной тепловой машины, работающей по обратному циклу Карно,

.

По обратному циклу Карно работают все холодильные машины.

15. Энтропия

Для описания термодинамических процессов широко используется понятие энтропии.

Отношение (приведенное количество теплоты) в обратимом процессе является полным дифференциалом и есть функция состояния системы, называемая энтропией S. Это непосредственно следует из равенства Клаузиуса, т. е. . (56)

Докажем, что в любом обратимом круговом процессе

. (57)

Для доказательства рассмотрим идеальный газ. Согласно первому началу термодинамики

. (58)

Используя уравнение Менделеева – Клапейрона перепишем (13.58) в виде

. (58^*)

В обратимом процессе при переходе идеального газа из состояния 1 в 2 интеграл не зависит от вида процесса перехода из 1 в 2, т. е.

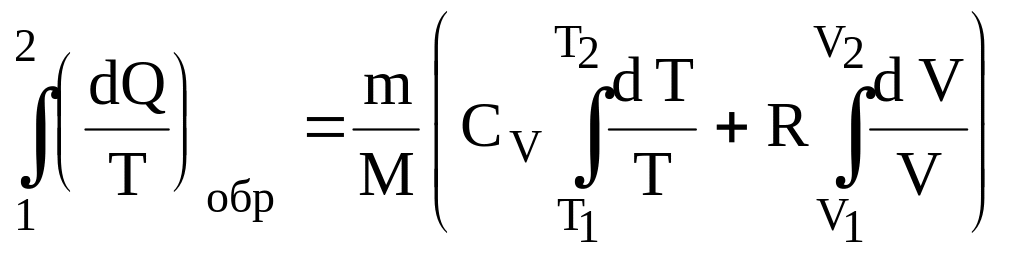(59)

или

. (60)

В случае кругового процесса V₂ = V₁, T₂ = T₁, то для идеального газа

.

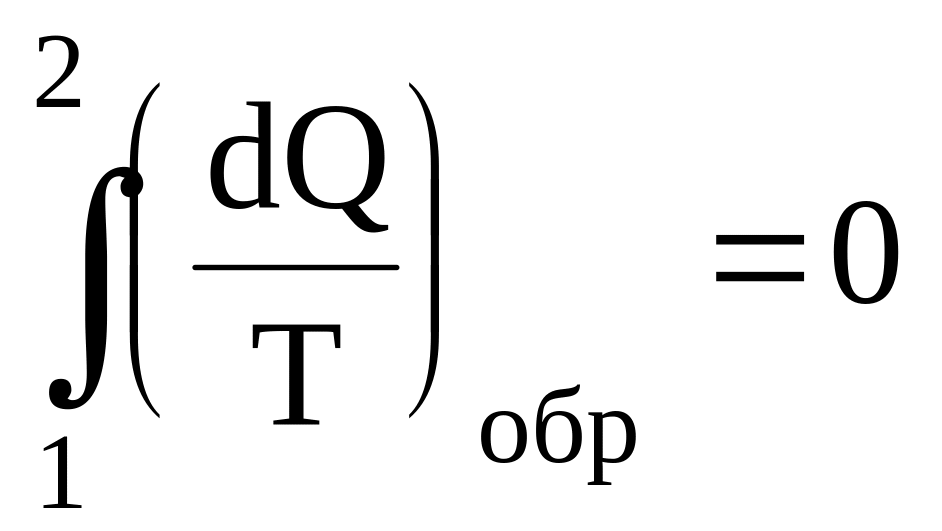Что же произойдет с энтропией системы?

Из анализа формул (58) и (58*) следует, что

(61)

или

. (62)

При неизменном числе молей идеального газа

.

После логарифмирования

(63)

или

С учетом последнего равенства формула (62) принимает вид

(64)

или

. (65)

При нагревании тела (dQ  0) его энтропия возрастает (dS  0); при охлаждении (dQ  0) энтропия тела убывает (dS  0). В процессе завершения обратимого цикла dS = 0, т. е. S = сonst. Энтропия изолированной системы в любом обратимом процессе остается постоянной.

Таким образом, энтропия физической системы есть функция ее состояния, и определяется с точностью до произвольной постоянной.

Разность энтропии в двух равновесных состояниях 1 и 2 равна приведенному количеству тепла, которое необходимо сообщить системе, чтобы перевести ее из состояния 1 в 2 по любому квазистатическому пути.

Рассмотрим физическую систему, которая необратимо переходит из равновесного состояния 1 в равновесное состояние 2 (рис. 11).При необратимом процессе перехода системы (на рис. 11 он изображен пунктирной линией 1– а – 2) из состояния 2, она переходит квазистатически по какому-либо пути, например, 2 – б – 1.

На основании неравенства Клаузиуса (54), имеем

. (66)

Учитывая, что процесс (2–б –1) – квазистатический

, (67)

тогда неравенство Клаузиуса принимает вид

, (68)

где Т – абсолютная температура окружающей среды, которая отдает физической системе тепло dQ.

Рис. 11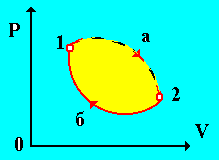

В случае адиабатически изолированной системы, для которой dQ = 0, в формуле (67) интеграл обращается в нуль, т. е.

S₂  S₁. (69)

Неравенство (13.69) выражает закон возрастания энтропии.

Следовательно, энтропия адиабатически изолированной системы не может убывать; она либо возрастает (необратимый процесс), либо остается постоянной (обратимый процесс). Понятие энтропии носит двойственный характер – макроскопический и микроскопический.

Соотношение = dS является макроскопическим определением энтропии.

Свойства энтропии.

1. Энтропия системы равна сумме энтропии каждого тела, т. е.

.

2. Энтропия – функция состояния системы.

3. В равновесных процессах без передачи тепла энтропия физической системы не меняется.

4. Энтропия является монотонно возрастающей функцией внутренней энергии тела (при постоянном объеме).

5. При постоянном объеме (изохорический процесс) dQ = dU,

т. е.

Так как Т  0, то dS и dU имеют один и тот же знак.

Задание внутренней энергии тела как функции объема и энтропии полностью определяет свойства однородного тела, т. е. U = U(V, S).

6. Энтропия определяется с точностью до произвольной постоянной.