12. Круговые процессы (циклы)

При изучении законов термодинамики широко используют круговые процессы (циклы).

Рис. 8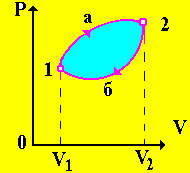

Термодинамический процесс, при котором система, претерпев ряд изменений, возвращается в исходное состояние, называют круговым процессом или циклом.

Физическую систему (например, идеальный газ), совершающую круговой процесс, называют рабочим телом.

Круговые процессы используют в основе работы всех тепловых машин: паровые и газовые турбины, двигатели внутреннего сгорания, холодильные машины и т. д.

Круговой процесс называют прямым (протекает по часовой стрелке), если после его завершения совершается положительная работа (рис. 8).

Рис. 9

Примером прямого цикла является процесс, совершающийся рабочим телом в двигателе, когда теплота от внешних источников поступает к рабочему телу, но часть ее отдается другим телам за счет совершения работы.

Круговой процесс называют обратным, если после его завершения (протекает против часовой стрелки) работа отрицательна (рис. 9).

Примерами обратного цикла является работа холодильных машин, когда рабочее тело передает теплоту от холодного тела к горячему за счет затраты работы внешних сил.

Термодинамическое состояние рабочего тела зависит от его внутренней энергии. Поэтому полное изменение внутренней энергии рабочего тела после завершения кругового цикла равно нулю, т. е.

U = 0.

Тогда согласно первому началу термодинамики

Q = A,

где Q – количество теплоты, переданное рабочему телу; А – работа, совершаемая за цикл рабочим телом.

В прямом цикле Q  0, т. е. к рабочему телу подводится больше теплоты, чем отводится.

Следовательно, работа А  0.

В обратном цикле Q  0. А^*= A < 0, где А^* – работа внешних сил.

13. Обратимый цикл Карно

Рассмотрим обратимый цикл Карно, совершающийся идеальной тепловой машиной. Цикл Карно состоит из четырех обратимых процессов: двух изотерм и двух адиабат. На рис. 10 приведен прямой цикл Карно.

Рис.10

1. Участок 1–2. Идеальный газ, находящийся в цилиндре под поршнем, в процессе изотермического расширения (Т₁ = сonst) приводится в тепловой контакт с нагревателем, который передает идеальному газу теплоту Q₁.

2. Участок 2–3. В состоянии 2 газ полностью теплоизолируется от нагревателя. Происходит адиабатическое расширение его, и температура понижается до Т₂.

3. Участок 3–4. В состоянии 3 идеальный газ приводится в контакт с холодильником. Происходит изотермическое сжатие (Т₂ = сonst), идеальный газ передает холодильнику теплоту Q₂.

4. Участок 4–1. В состоянии 4 газ теплоизолируется от холодильника. Затем происходит адиабатическое сжатие.

Температура газа повышается до Т₁.

Работа, совершаемая рабочим телом за цикл,

А = (Q₁  Q₂)  0 ,

где

А  Q₁. (49)

Следовательно, полезная работа меньше энергии, полученной в форме теплоты от нагревателя на величину теплоты, переданную холодильнику.

КПД идеальной тепловой машины, работающей по обратному циклу Карно можно вычислить, используя формулу

,

где А – полезная работа совершаемая за цикл; Q₁ – количество теплоты получаемое за цикл от нагревателя или

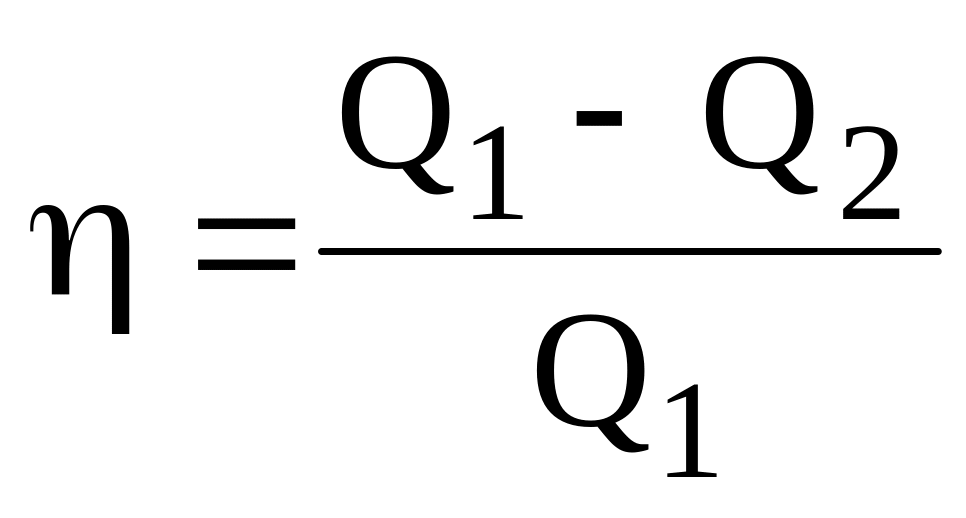, (50)

где А₁₂ = Q₁ – Q₂; Q₂ – количество теплоты, отданное за цикл холодильнику.

На участке 1 – 2 (изотермическое расширение dU = 0) согласно I начала термодинамики

, (51)

где m – масса идеального газа; М – молярная масса газа; R – универсальная газовая постоянная; Т₁ – температура изотермического расширения; V₁ – объем газа в начальном состоянии 1; V₂ – объем газа в состоянии 2.

На участке 3–4 (изотермическое сжатие dU = 0) согласно I начала термодинамики

, (52)

где m – масса идеального газа; М – молярная масса газа; R – универсальная газовая постоянная; Т₂ – температура изотермического сжатия; V₃ – объем газа в состоянии 3; V₄ – объем газа в состоянии 4.