После интегрирования (26) с учетом (27), получим

или

. (28)

Выражение (28) называют уравнением адиабаты (уравнение Пуассона).

Используя уравнение Менделеева – Клапейрона, перепишем (28) в виде

Рис. 7

Р – V диаграмма адиабатического процесса приведена на рис. 2.7.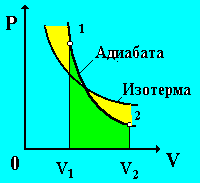

На рис. 7 видно, что кривая адиабаты идет круче, чем изотерма. Объясняется это тем, что при адиабатическом расширении идеального газа происходит не только уменьшение давления, но и понижение температуры, так как внутренняя энергия газа убывает. При адиабатическом сжатии газа растут давление и температура, не только из-за уменьшения объема, но и из-за увеличения внутренней энергии.

После интегрирования выражения (21) получим формулу работы идеального газа в адиабатическом процессе

. (29)

Графически работа при адиабатическом процессе численно равна площади криволинейной трапеции (рис. 7, штрихованная часть графика).

Используя уравнение Майера (16) и формулу (27), получаем

. (30)

Тогда работа

(31)

или

, (32)

или

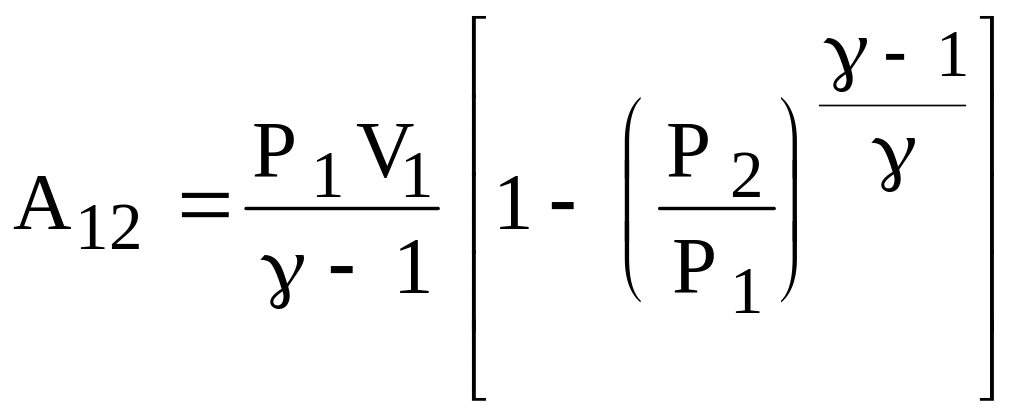, (33)

где Р₁, V₁, T₁ , Р₂, V₂, T₂ – давление, объем и температура идеального газа, соответственно в первом и втором состояниях.

9. Адиабатическое сжатие и расширение звуковых волн

Воспринимаемые нашими органами слуха звуковые волны при распространении сжимаются и расширяются почти адиабатически (квазиадиабатически), так как чередование сжатия и разрежения, при распространении звуковых волн, происходит очень быстро.

При сжатии газа его температура повышается до тех пор, пока теплота не начнет поступать наружу. Если же газ расширяется, то его температура понижается до тех пор, пока в систему не начнет поступать теплота извне.

В звуковой волне, воспринимаемой ухом, теплопроводность воздуха мала, а расстояние между соседними областями сжатия и расширения относительно велики (/2, где  – длина волны). Все это происходит быстро, т. е. процесс адиабатический. Это используется при определении скорости распространения звука. Скорость звука

где – модуль всестороннего сжатия (коэффициент объемной упругости).

Дифференцируя уравнение Пуассона (10.28) по объему, получим

= 0,

т. е. К = Р. Следовательно, скорость звука . (34)

Для воздуха при нормальных условиях;  = 1,4;  = 1,29 кг/м³.

v_зв  331 м/c, что хорошо согласуется с данными эксперимента.

11. Обратимые и необратимые процессы

Для описания термодинамических процессов недостаточно одного первого начала термодинамики, так как оно ничего не говорит о направлении протекания процессов. Например, самопроизвольный процесс передачи теплоты от холодного тела к горячему невозможен.

Термодинамический процесс называют обратимым, если он протекает столь медленно, что его можно рассматривать как непрерывный ряд равновесных состояний.

Этот процесс перехода термодинамической системы из одного равновесного состояния в другое, допускает возвращение ее в первоначальное состояние, через ту же последовательность промежуточных состояний, что и в прямом процессе, но происходящем в обратном порядке.

Примером обратимого процесса являются незатухающие колебания тела на пружине в вакууме. Термодинамический процесс, протекающий с конечной скоростью и сопровождающийся рассеянием энергии (из-за трения, теплопроводности и т. п.) называют необратимым. Примером необратимого процесса является, например, торможение тел под действием сил трения. Вообще все процессы, связанные с трением и сопротивлением движению, являются необратимыми.

Из необратимости термодинамических процессов следует, что в прямом направлении, они протекают самопроизвольно; в обратном направлении требуются затраты энергии, т. е. компенсирующие процессы.