6. Уравнение Майера
Найдем связь между Ср и Сv идеального газа. Используя формулы (14), (16), (17), запишем первое начало термодинамики в виде
или
Ср = Сv + R. (20)
Формулу (20) называют уравнением Майера.
7. Применение первого начала термодинамики
для изотермического процесса
При изотермическом расширении (сжатии) газа происходит переход его из состояния 1 в 2 при постоянной температуре, т. е.
Рис.
5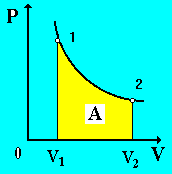
Примерами изотермического процесса являются кипение, конденсация, плавление и кристаллизация химически чистых веществ, при постоянном внешнем давлении. Внутренняя энергия идеального газа при изотермическом процессе не изменяется, т. е.
Первое начало термодинамики для изотермического процесса записывают в виде dQ = dA, так как все подведенное к системе тепло идет на совершения системой работы.
Молярная теплоемкость идеального газа в изотермическом процессе
С
=
,
так как dQ
0, dT
= 0, dU
= 0.
Работа изотермического процесса можно определить по формуле
Окончательно
Графически работа в изотермическом процессе изображается площадью криволинейной трапеции (заштрихованная часть на рис. 5).
8. Применение первого начала термодинамики
для адиабатического процесса
Термодинамический процесс, в котором система при переходе из состояния 1 в состояние 2 не обменивается теплотой с окружающей средой, называют адиабатическим.
На практике адиабатический процесс можно осуществить при быстром расширении (сжатии) газа, когда Q 0. Например, быстро протекающее расширение газов в цилиндре двигателя внутреннего сгорания.
В двигателе Дизеля воздух быстро сжимается адиабатически в 15 и более раз, чем в двигателе внутреннего сгорания. При этом температура воздуха повышается до 3000 оС, поэтому при впрыскивании горючей смеси происходит ее самовоспламенение. При возникновении ударной волны газ адиабатически сжимается и сильно нагревается, так как он не успевает отдать выделившуюся теплоту. Метеориты при вхождении в атмосферу оплавляются и испаряются в основном по этой причине, а не из-за наличия трения и сопротивления при движении в атмосферном воздухе. Адиабатическое расширение приводит к охлаждению системы, что используется при сжижении газов (адиабатическое размагничивание парамагнитных солей позволяет получить температуры, близкие к абсолютному нулю). К адиабатическим процессам относится и свободное расширение газов (рис. 6), так как Q = const, А = 0, U = 0, T = 0.Теплоемкость вещества при адиабатическом процессе С = 0 ( dT 0).
Первое начало термодинамики для адиабатического процесса представим в виде
dU = dA (21)
или
.
Следовательно, при адиабатическом процессе газ совершает работу за счет убыли его внутренней энергии.
Рис. 6
Для
одного моля идеального газа
изменение внутренней энергии
dU = CVdT. (22)
При этом газ совершит работу dA = PdV. Согласно (2.20), получаем
CVdT + PdV = 0 (23)
Используя
уравнение Менделеева – Клапейрона и
уравнение Майера, получаем
.
(24)
На основании формул (23) и (24) после преобразований имеем
Ср РdV + Cv VdP = 0. (25)
Уравнение (25), представим в виде
,
(26)
Где Ср/Cv = . (27)
называют коэффициентом Пуассона (показателем адиабаты).