15. Дифракция Фраунгофера от щели.

Дифракция Фраунгофера – это дифракция в параллельных лучах, т.е. когда экран далеко от препятствия.

Рассмотрим бесконечно узкую щель шириной b, на которую нормально падает плоская волна. Для анализа дифракции разобьём световую волну, падающую на щель на число N параллельных лучей с малой разность фаз между соседними лучами и воспользуемся формулой для интенсивности полученной при рассмотрении многолучевой интерференции

, где - интенсивность одного луча.

Между 1 и 2 . Этому соответствует разность фаз => => . Если φ=0, то по первому замечательному пределу . В центре дифракционной картину – максимум. Если же , то – условие минимума.

Если же принимает максимальное значение, то получим условие максимумов, т.е. . Условия максимумов мы можем получить, разбивая щель на зоны Френеля. В щели будет укладываться зон Френеля. Если оно чётное, то мы получаем условие минимума , если же нечётное – максимума .

В направлении угла φ=0 вся щель действует как одна зона Френеля => I-максимально.

Т.к. φ≤90⁰, то для m=1 видно, что дифракционная картина из многих минимумов и максимумов при b < λ не появляется.

График интенсивности щели в зависимости от угла щели имеет вид:

Количество критериев, позволяющим определить вид дифракции (Фраунгофера или Френеля) будет наблюдаться на опыте.

16. Дифракционная решетка.

Дифракционная решетка  совокупность большого числа регулярно расположенных одинаковых параллельных друг другу щелей шириной а, разделенных непрозрачным промежутком b, нанесенных на плоскую или вогнутую (выпуклую) поверхность.

Решетка характеризуется периодом d = a + b, числом щелей на единицу длины n = 1/d и общим числом щелей N. Общая длина решетки L = Nd.

Различают амплитудные и фазовые дифракционные решетки.

У амплитудной дифракционной решетки периодически изменяется коэффициент отражения или пропускания, что приводит к изменению амплитуды падающей волны. У фазовой дифракционной решетки штрихи имеют специальную (например, треугольную) форму, которая изменяет фазу световой волны.

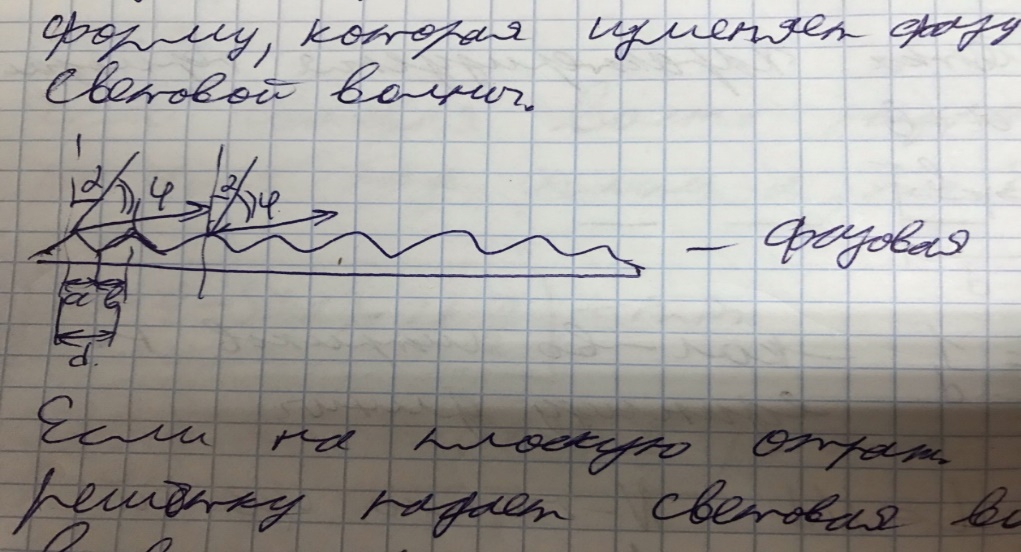
Если на плоскую отражающую решётку падает световая волна в виде параллельного пучка лучей, то в результате интерференции когерентных лучей от всех N штрихов решётки пространственное (по углам) распределение интенсивности света можно представить в виде

.

определяет интенсивность света при дифракции на 1 штрихе, а интенсивность обусловлена интерференцией N когерентных лучей от всех штрихов решётки.

Для данной длины волны  функция определяется периодом d, полным числом штрихов N, углом падения α и углом дифракции φ, и не зависит от формы штрихов.

Оптическая разность хода:

=d(sinα+sinφ)

Функция есть периодическая с регулярной интенсивностью главных максимумов и вторичных максимумов малой интенсивности.

d(sinα+sinφ)=±2m – max d(sinα+sinφ)=±(2m+1) – min

При нормальном падении монохроматического света на прозрачную дифракционную решётку на экране возникает дифракционная картина.

dsinφ=±2m – max dsinφ=±(2m+1) – min

Если для расчёта использовать метод зон Френеля, то нужно разделить каждую щель на Z зон. Если количество зон чётное, то минимум, если нечётное, то каждая из них становится источником монохроматического света.

Угловая дисперсия характеризует степень пространственного разделения лучей с разной длиной волны.

dsinφ=m