12. Принцип Гюйгенса – Френеля.

Дифракция - любое отклонение при распространении волны от законов геометрической оптики.

Благодаря дифракции световые волны (как и любые другие волны, например, акустические) могут попадать в область геометрической тени: огибать препятствия, распространяться вдоль поверхностей, проникать сквозь малые отверстия, размеры которых сравнимы или меньше длины волны.

Для объяснения дифракции света (волновая природа света) используют принцип Гюйгенса-Френеля: каждая точка фронта волны является источником вторичных волн, которые когерентны и интерферируют.

13. Зоны Френеля.

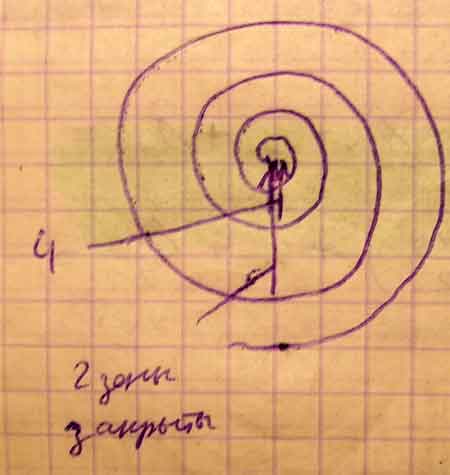
Согласно этому методу в любой момент времени волновую поверхность S разбивают на отдельные зоны, каждая из которых отделена от предыдущей на λ/2.

При распространении плоской монохроматической электромагнитной волны в т. М на экране наблюдается дифракция света в виде чередующихся светлых и темных колец.

Н а произвольной волновой поверхности S, находящейся на расстоянии r0 (ОМ) от экрана, выделим зоны, которые в данном случае, образуют ряд концентрических окружностей (колец). Границей первой (центральной) зоны служат точки поверхности S, находящейся на расстоянии r₁=r₀+λ/2 от точки М. Соответственно точки В, С волновой поверхности, находящиеся на расстоянии r₁ = r₀+ λ, r₃=r₀+3 λ /2 и т. д. от т. М, образуют границы второй, третьей и т.д. зон Френеля. Радиусы зон Френеля, для любой m-й зоны Френеля , где m = 1, 2, 3…

Площади всех зон Френеля равновелики (S m=πr₀ λ) и содержат одинаковое количество вторичных источников. Вторичные волны, возбуждаемые в т. М от двух соседних зон, противоположны по фазе и при наложении гасят друг друга. Так как оптическая разность хода δ в т. М равна нечетному числу длин полуволн (условие минимума интерференции).

Результирующая амплитуда A= A1/2+(A1/2-A2+A3/2) + (A3/2-A4+A5/2) +⋯=A1/2. Чередование знаков вызвано тем, что соседние зоны гасят друг друга.

Так как все выражения, стоящие в скобках, равны нулю то, при полностью открытом фронте волны амплитуда результирующей волны равна половине амплитуды первой зоны Френеля.

14. Дифракция Френеля от простейших преград.

Дифракция Френеля – это дифракция сходящихся лучей. Наблюдается на близком расстоянии от препятствия.

Качественно явление дифракции объясняется принципом Гюйгенса: каждая точка фронта волны становит источником вторичных сферических волн, и фронт новой волны является огибающей этих вторичны волн.

Дифракция на круговом отверстии.

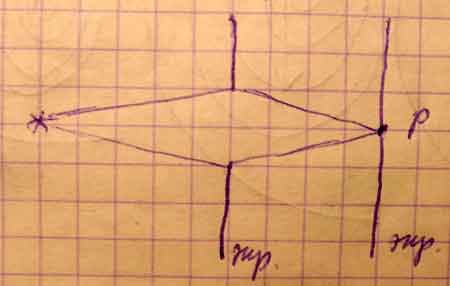
В центре дифракционной картины (в Р) будет наблюдаться тёмное пятно (минимум I), если в отверстии укладывается чётное число зон Френеля. Максимум наблюдается (светлое пятно), если в отверстии укладывается нечётное число зон.

Пусть n –чётное число, тогда

Если n=2, то – мало.

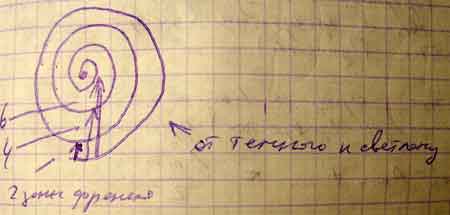
Пусть n – нечётное, тогда .

Если n=2, то – большое.

Дифракция на круговом диске.

Особенностью дифракции сферических волн от точечного источника на непрозрачном диске является присутствие в центре геометрической тени светлого пятна (пятна Пуассона).

Амплитуда в данной точке определяется первой открытой зоной Френеля. Пусть m-число зон Френеля, тогда A=