16. Момент сил, действующий на контур с током

Если контур с током (I = const) поместить в неоднородное внешнее магнитное поле, то на него будет действовать сила Ампера, т. е.

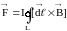. (6.76)

В однородном магнитном поле результирующая сила Ампера, действующая на контур с током, равна нулю:

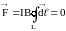. (6.77)

Рассмотрим плоский контур с током малых размеров (магнитный листок), который называют элементарным. Такой контур характеризуют вектором магнитного момента

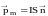, (6.78)

Рис. 6.24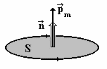

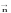
где I  сила тока в витке; S  площадь витка ограниченного контуром L;  вектор нормали, направление которого связано с направлением тока в витке правилом правого винта (рис. 6.24).

По модулю

р_m = IS. (6.79)

В СИ магнитный момент измеряется в амперах на метр в квадрате (Ам²).

Если контур не плоский, то

, (6.80)

где интеграл зависит только от выбора контура L, на который натянута поверхность S. Расчеты показывают, что эту силу можно записать в виде

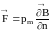, (6.81)

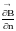
где р_m  модуль магнитного момента контура;  частная производная вектора 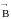по направлению вектора нормали 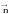(по направлению ).

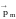Проекция силы, например, на направление оси Х

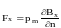. (6.82)

В однородном магнитном поле F = 0, так как 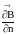= 0.

Результирующий момент сил Ампера, действующий на контур, запишем в виде

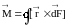(6.83)

или в ви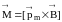де

, где 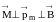(рис. 6.25). (6.84)

Рис. 6.25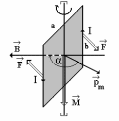

Пара сил Ампера действует на стороны b контура; на стороны а контура действуют силы, стремящиеся только растянуть его, на рис. 6.25 они не показаны. По модулю вращающий момент сил Ампера

М = р_mВsin = ISBsin, (6.85)

где   угол между векторами и .

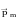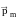При  = 0^о, М = 0 (  ) положение контураустойчиво. При  = 180^о, М = 0 (  ) положение контура  неустойчиво.

Если магнитное поле неоднородно и размеры контура малы, то влиянием неоднородности можно пренебречь.

Билет №11

1. Электроёмкость, конденсаторы. Электроёмкость проводящего шара. Ёмкость плоского конденсатора, сферического конденсатора, цилиндрического конденсатора

Электрическая емкость проводников

Рассмотрим проводник, изолированный от влияния других проводников и заряженных тел. При сообщении заряда q проводнику возникает потенциал, пропорциональный этому заряду (  q). Опыт показывает, что отношение заряда проводника к его потенциалу уже не зависит ни от заряда, ни от потенциала, является для данного проводника величиной постоянной, которую называют электрической емкостью проводника С (емкостью), т. е.

С = q /  (4)

Найдем емкость проводящего шара радиуса R.

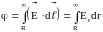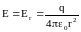
Потенциал на поверхности заряженного шара можно найти т. е. , где  напряженность поля заряженной сферы (при r = R); _ = 0.