Закон Ома для неоднородного участка цепи

Рассмотрим неоднородный участок цепи 1–2 на котором присутствуют силы неэлектрического происхождения (сторонние силы).

Обозначим через ε₁₂ – ЭДС на участке 1–2; Δϕ =ϕ₁ −ϕ₂ – приложенную на концах участка разность потенциалов.

Если участок 1–2 неподвижен, то (по закону сохранения энергии) общая работа  A₁₂ сторонних и электростатических сил, совершаемая над носителями тока, равна теплоте Q, выделяющейся на участке.

Работа сил по перемещению заряда q₀ :    A₁₂ = q0 ⋅ε₁₂ + q₀ ⋅Δϕ .

ЭДС ε₁₂ , как и сила тока I, – величина скалярная. Если ЭДС способствует движению положительных зарядов в выбранном направлении, то ε₁₂ > 0, если препятствует, то ε12 < 0.

За время t в проводнике выделится теплота:   Q = I² ⋅ R ⋅ t = I ⋅ R ⋅ (I ⋅ t) = I ⋅ R ⋅ q₀ .

Отсюда следует закон Ома для неоднородного участка цепи в интегральной форме, который является обобщённым законом Ома:

Частные случаи: 1. Если на данном участке цепи источник тока отсутствует, то мы получаем закон Ома для однородного участка цепи: I=U/R. 2. Если цепь замкнута (Δϕ = 0), то получаем закон Ома для замкнутой цепи:

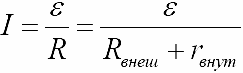 ,где ε – ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи, R_внеш – сопротивление внешней цепи, r_внут – внутреннее сопротивление источника тока.

3. Если цепь разомкнута, то I = 0 и ε₁₂ =ϕ₂ −ϕ₁ , т.е. ЭДС, действующая в разомкнутой цепи равна разности потенциалов на её концах.

4. В случае короткого замыкания сопротивление внешней цепи R_внеш = 0 и сила тока I=ε/rвнут в этом случае ограничивается только величиной внутреннего сопротивления источника тока.

Билет №3

1. Поток вектора напряжённости электрического поля. Теорема Гаусса

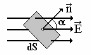
Электрическое поле обладает важным свойством: потоком вектора напряженности (потоком вектора ).

Потоком вектора напряженности электрического поля называют интеграл по поверхности от скалярного произведения векторов и dS .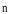

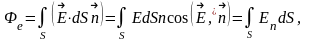(1)

где Е_n  проекция вектора 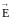на нормаль .

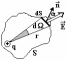
Для того чтобы найти поток вектора , окружим точечный заряд произвольной замкнутой поверхностью S (рис. 2).

По определению поток вектора

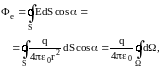(3)

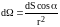
где  телесный угол, опирающийся на элемент dS поверхности S, с вершиной в точке расположения заряда q;

Работа, мощность, КПД источника тока. Тепловое действие тока. Закон Джоуля-Ленца

Рассмотрим однородный участок 1-2 проводника, к которому приложена разность потенциалов ₂ - ₁. Если по проводнику течет ток I, то за время dt через поперечное сечение его будет перенесен заряд dq = Idt.

Следовательно, силы поля совершат элементарную работу

А= Iut = I²Rt

Если электрическая цепь замкнута и содержит источника с ЭДС 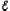, то вся затраченная источником тока работа А_З = А_П + А_ВНУТ,

где А_З = I t, А_П = IU_Rt, А_ВНУТ = IU_rt.

Тогда = U_R + U_r = IR+ Ir,

где U_R - напряжение на внешнем сопротивлении, U_r - напряжение на внутреннем сопротивлении источника тока.

Мощность тока можно найти по формуле N =

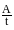
Развиваемая источником тока затраченная мощность

N_З = N_П + N_ВНУТ, (5.22)

где N_З= I , N_П = IU_R, N_ВНУТ = IU_r.

КПД источника тока можно найти по формуле

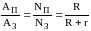 = . (5.23)

Затраченная источником тока мощность

N_З = I =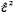 /(R+r), (5.24)

где I = /(R + r).

Полезная мощность, выделяемая во внешнем участке цепи

N_П = IU_R = I²R = .

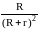
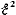Тепловое действие тока. Закон Джоуля – Ленца.

При прохождении тока по проводнику происходит его нагревание, т. е. выделяется некоторое количество теплоты Q. Вся работа сторонних сил идет на выделение тепла.

.

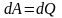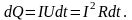
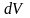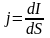Если на участке выделяется объем , то с учетом выражений

и

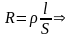
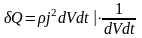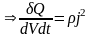. (удельная тепловая мощность)

;

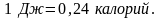
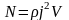
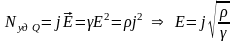Билет №4

1.Применение теоремы Гаусса для расчёта электрических полей. Типы распределения заряда. Поле бесконечной равномерно заряженной плоскости

В симметричных точках этого поля вектор равен по модулю и противоположен по направлению. В связи с этим в качестве замкнутой поверхности можно выбрать цилиндрическую (рис. 3). Полный поток вектора пронизывающий

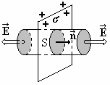
Ф_е = 2ЕS.

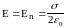, (13)

где Е_n  проекция вектора на нормаль (  , рис. 3).

Если   0, то Е_n  0, т. е. вектор направлен от заряженной плоскости (линии напряженности начинаются на положительных зарядах).

Если   0, то Е_n  0, т. е. вектор форме направлен к заряженной плоскости (линии напряженности оканчиваются на отрицательных зарядах).

Согласно (13) напряженность электростатического поля, созданного равномерно заряженной бесконечной плоскостью, не зависит от расстояния до нее, а поле является однородным справа и слева от плоскости.

2. Работа, мощность, КПД источника тока. Тепловое действие тока. Закон Джоуля-Ленца.

Рассмотрим однородный участок 1-2 проводника, к которому приложена разность потенциалов ₂ - ₁. Если по проводнику течет ток I, то за время dt через поперечное сечение его будет перенесен заряд dq = Idt.

Следовательно, силы поля совершат элементарную работу

А= Iut = I²Rt

Если электрическая цепь замкнута и содержит источника с ЭДС , то вся затраченная источником тока работа А_З = А_П + А_ВНУТ,

где А_З = I t, А_П = IU_Rt, А_ВНУТ = IU_rt.

Тогда = U_R + U_r = IR+ Ir,

где U_R - напряжение на внешнем сопротивлении, U_r - напряжение на внутреннем сопротивлении источника тока.

Мощность тока можно найти по формуле N =

Развиваемая источником тока затраченная мощность

N_З = N_П + N_ВНУТ, (5.22)

где N_З= I , N_П = IU_R, N_ВНУТ = IU_r.

КПД источника тока можно найти по формуле

 = . (5.23)

Затраченная источником тока мощность

N_З = I = /(R+r), (5.24)

где I = /(R + r).

Полезная мощность, выделяемая во внешнем участке цепи

N_П = IU_R = I²R = .

Тепловое действие тока. Закон Джоуля – Ленца.

При прохождении тока по проводнику происходит его нагревание, т. е. выделяется некоторое количество теплоты Q. Вся работа сторонних сил идет на выделение тепла.

.

Если на участке выделяется объем , то с учетом выражений

и

. (удельная тепловая мощность)

;

Билет №5

1. Поле двух бесконечных, разноимённо заряженных плоскостей. Поле равномерно заряженной сферической поверхности. Поле равномерно заряженного шара. Напряжённость электрического поля бесконечной равномерно заряженной нити