КР2

10

Контрольная работа №2

Вариант 6

206. В сосуде находится 65 г кислорода. Найти число молекул, находящихся в сосуде.

Число молекул газа:

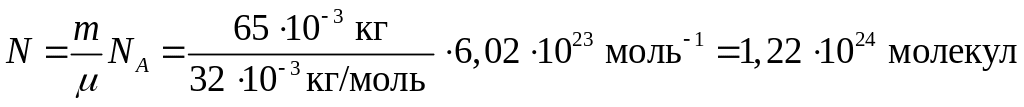
где молярная масса O₂; число Авогардо.

Ответ:

216. Какой энергией теплового движения обладает газ, занимающий объем 86 см³ при давлении 23 мм рт. ст? Молекулы газа двухатомные.

Внутренняя энергия газа:

(1)

где число степеней свободы молекулы газа (для двухатомного газа ); масса газа; молярная масса газа; универсальная газовая постоянная.

Уравнение состояния газа:

(2)

Из (1) и (2) находим:

Ответ:

226. Атмосферное давление на поверхности Земли 0,1 МПа. На сколько изменится давление при подъеме наблюдателя на высоту 119 м? Температуру воздуха считать постоянной и равной 290 К. (Массу одного киломоля воздуха принять равной 29 кг).

Давление на высоте

Давление увеличится на

Ответ:

236. Определить массу одной из пылинок, взвешенных в воздухе, если в толщине слоя воздуха 3 см их концентрация различается на 35% при температуре 22°С.

Концентрация пылинок на высоте

(1)

где ускорение свободного падения; постоянная Больцмана.

По условию задачи:

(2)

Из(1) и (2) находим:

Ответ:

246. Найти для кислорода отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме.

Молярные теплоемкости кислорода:

при :

(1)

при :

(2)

где число степеней свободы молекулы газа (для двухатомного газа ); универсальная газовая постоянная.

Удельные теплоемкости кислорода:

(3)

(4)

где молярная масса газа.

Отношение удельных теплоемкостей:

Ответ:

255. Какая доля теплоты, подводимой к идеальному газу, расходуется на увеличение внутренней энергии газа? Газ одноатомный, процесс изобарический.

Увеличение внутренней энергии газа:

(1)

где (2) – молярная теплоемкость газа при постоянном объеме; – число молей газа; – изменение температуры газа; число степеней свободы молекулы газа (для одноатомного газа ); универсальная газовая постоянная.

Поглощенное тепло в изобарическом процессе:

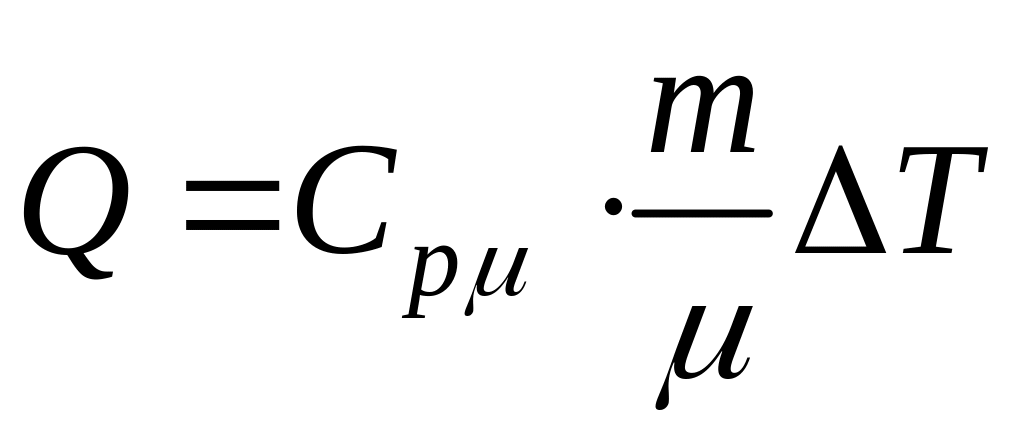
где – (4) – молярная теплоемкость при постоянном давлении.

Тогда

Ответ:

266. Идеальная холодильная машина работает как тепловой насос по обратному циклу Карно. При этом она берет теплоту от воды с температурой 3°С и передает ее воздуху с температурой 27°С. Найти коэффициент – отношение теплоты, переданной за некоторый промежуток времени воздуху к работе машины за это же время.

К.п.д. прямого цикла:

(1)

где совершенная работа; тепло полученное от нагревателя; тепло, отданное холодильнику.

Для обратного цикла Карно:

тепло, переданное более горячему телу; тепло, отнятое у холодильника.

По условию задачи необходимо найти отношение теплоты, переданной за некоторый промежуток времени воздуху к работе машины за это же время. Количество теплоты вместе с работой внешних сил равно количеству теплоты т.е. или .

Тогда

(2)

Сравнивая формулы (1) и (2), видим, что

Ответ:

276. Найти изменение энтропии при изобарическом расширении азота массой 28 г от объема до объема .

Элементарное изменение тепла при изобарическом процессе:

(1)

где – молярная теплоемкость при постоянном давлении (2)

число степеней свободы молекулы газа (для двухатомного газа ).

Элементарное изменение энтропии:

(3)

(4)

Универсальный газовый закон:

(5)

Из (5): (6)

Подставим (6) в (4):

Ответ: .