
КР1
.pdf
11
166. На краю свободно вращающегося горизонтального диска (радиус 3 м, момент инерции 142 кг · м2) стоит человек массой 80 кг. Во сколько изме-
нится кинетическая энергия системы (W2 /W1 ), если человек перейдет от края диска к центру? Момент инерции человека рассчитать как для материальной точки.
R =3 м
I0 =142 кг м2 т=80 кг
W2 =?
W1
Момент инерции человека, стоящего на краю диска:
I = mR2 (1)
Начальный момент инерции системы:
I = I |
0 |
+ I = I |
0 |
+mR2 |
|
|
(2) |
||||
1 |
|
|
|
|
|
|
|
|
|
||
Начальная кинетическая энергия системы: |
|
||||||||||
W = |
|
I ω2 |
(I0 |
+ mR2 ) |
ω |
2 |
(3) |
||||
|
|
1 1 |
= |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
1 |
|
|
2 |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
где ω1 – начальная угловая скорость вращения платформы. Конечный момент инерции системы: I2 = I0 (4)
Закон сохранения момента импульса:
I1ω1 = I2ω2
Из (5) конечная угловая скорость платформы:
ω |
|
=ω |
I |
=ω |
I |
0 |
+mR2 |
|
1 |
|
|
||||
|
|
|
|
I0 |
|||
|
2 |
1 I2 |
1 |
|
|
||
Конечная кинетическая энергия системы:
W2 = |
I ω2 |
|
I |
0 |
|
I |
0 |
+mR2 2 |
2 |
|||
2 2 |
= |
|
|
|
|
|
|
ω1 |
||||
2 |
2 |
|
|
I |
|
|||||||
|
|
|
|
|
0 |
|
|
|||||
(5)
(6)
(7)
12
Отношение энергий: |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
I |
0 |
|
I |
0 |
+mR2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ω1 |
|
|
|
|
|
|
2 |
+80 кг (3 м) |
2 |
|
||
W2 |
|
|
2 |
|
|
|
I0 |
|
I0 |
+mR2 |
|
142 кг м |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
=6 раз |
|||||||||||
W1 = |
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|||||||||
|
|
|
(I0 +mR2 ) |
ω |
2 |
|
I0 |
|
142 кг м2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: W2 |
=6 раз. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
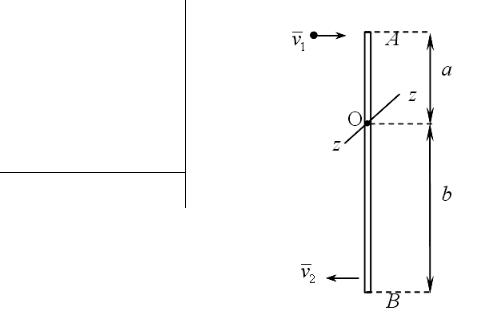
176. Однородный стержень массой 585 г и длиной АВ = 0,5 м может свободно вращаться вокруг горизонтальной оси z , проходящей через точку О. В точку А на конце стержня попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси z ) со скоростью 1 м/с и прилипает к стержню. Масса шарика 17 г. Определить линейную скорость точки В конца стержня, сразу после прилипания шарика, если расстояние АО = АВ/3.
M1 =17 г =0,017 кг
v1 =1 м/с
М2 =585 г =0,585 кг АВ =0,50 м =l
a = 13 l
v2 =?
Закон сохранения момента импульса: |
|
M1v1a =(I0 + M1a2 )ω |
(1) |
где M1v1a – момент импульса пластилинового шарика относительно оси z;
(I0 +M1a2 )ω – момент импульса системы относительно оси z.
Момент инерции стержня относительно точки О:
|
1 |
|
|
|
l |
2 |
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
M |
2 |
|
|
|
|
|
M |
2 |
3 |
|
3 |
l |
|
|
|
1 |
|
8 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
I0 = |
|
|
|
3 |
|
+ |
|
|
|
|
= M2l |
2 |
+ |
= |
M |
2l |
2 |
(3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
81 |
|
9 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|
|
|
|
|
|||||
Из (1) находим угловую скорость вращения, подставляя (2):
|
|
M1v1a |
|
|
|
M v |
l |
|
|
|
|
|
|
3M1v1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ω = |
|
= |
|
|
|
|
1 1 3 |
|
|
|
|
|
= |
(4) |
|||
I0 |
+ M1a2 |
|
|
|
|
|
|
l |
2 |
l (M1 + M2 ) |
|||||||
|
1 |
M |
2l |
2 |
+ M1 |
|
|
||||||||||
|
|
|
9 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||
14
Линейная скорость точки В:
v =ω b = |
3M1v1 |
2 l = |
2M1v1 |
= |
2 0,017 кг 1 м/с |
=0,056 м/с |
|
|
|
|
|||||
2 |
l (M1 |
+ M2 ) |
3 |
M1 + M2 |
|
0,017 кг +0,585 кг |
|
|
|
||||||
Ответ: v2 =0,056 м/с.
