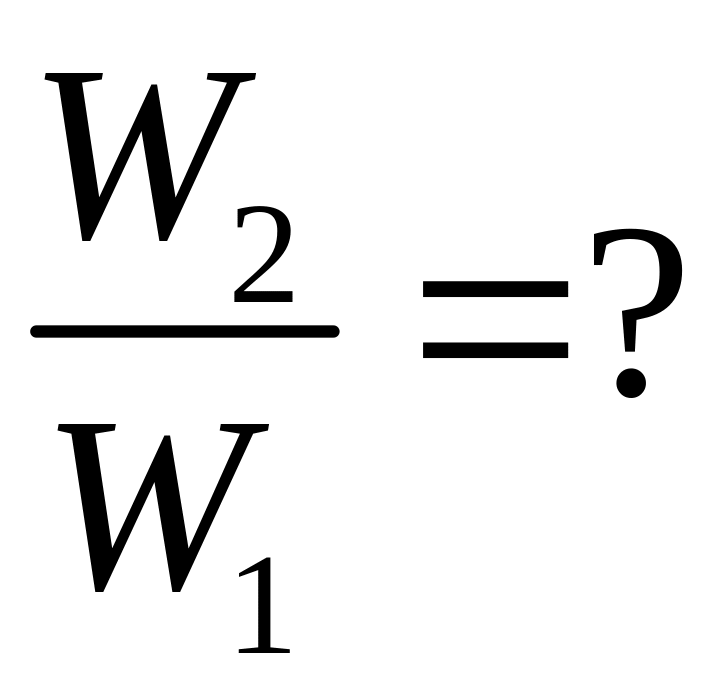КР1

13

Контрольная работа №1

Вариант 6

108. С балкона бросили мячик вертикально вверх с начальной скоростью 6 м/с. Через 7 с мячик упал на Землю. Определить скорость мячика в момент удара о Землю.

Скорость движения мячика:

(1)

где ускорение свободного падения.

В момент удара о землю:

Знак «–» говорит о том, что скорость противоположна по направлению.

Ответ:

112. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, меньше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 10° с вектором линейной скорости.

Тангенциальное ускорение направлено по касательной к траектории; нормальное ускорение направлено к центру кривизны траектории. Векторы и взаимно перпендикулярны.

Из геометрии рисунка находим:

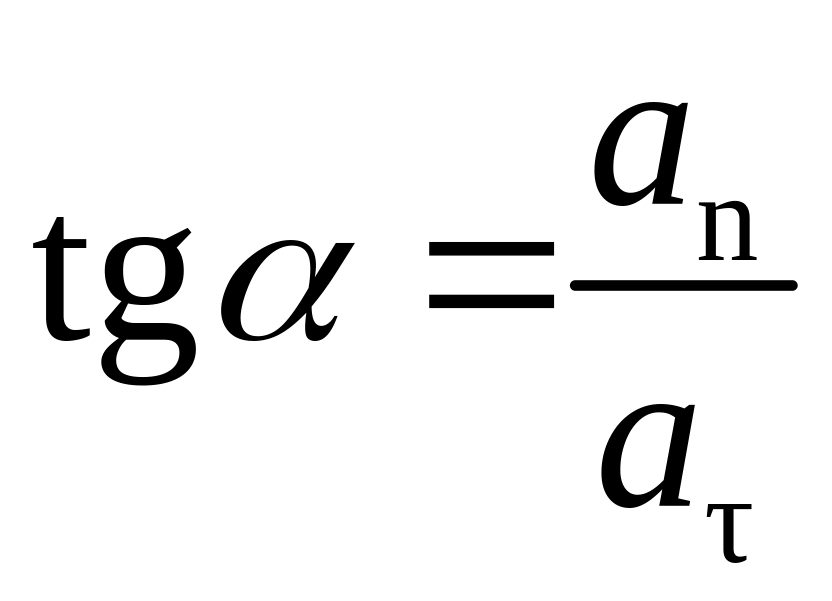
Отсюда

Ответ:

128. Масса лифта с пассажирами равна 800 кг. Найти, с каким ускорением, и в каком направлении движется лифт, если известно, что натяжение троса, поддерживающего лифт, равно 11,76 кН.

Предположим, что кабина движется вверх.

Уравнение движения:

(1)

где ускорение свободного падения; ускорение груза; сила натяжения троса; сила тяжести.

Из (1) ускорение лифта:

Ответ: лифт движется вверх с ускорением 4,9 м/с².

135. Вверх по наклонной плоскости с углом наклона 31° пущена шайба, через некоторое время она останавливается и движется вниз. Определить коэффициент трения шайбы о плоскость, если время спуска в два раза больше времени подъема.

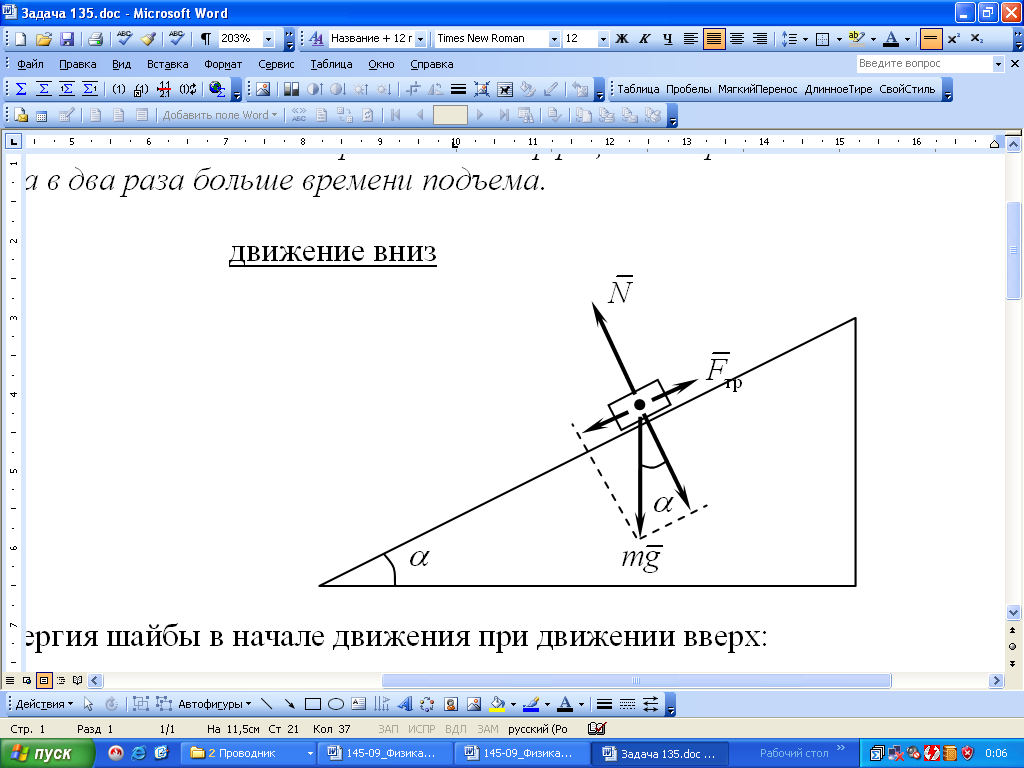
Кинетическая энергия шайбы в начале движения при движении вверх:

(1)

где т – масса шайбы.

Кинетическая энергия шайбы в конце движения при движении вниз:

(2)

Работа против сил трения: (3)

где S – длина плоскости.

Закон сохранения энергии:

(4)

С другой стороны: (5)

(6)

Из (5) и (6) находим: (7)

Из (4), подставляя (7) получим:

(8)

Уравнение движения вниз:

(9)

где а – ускорение шайбы.

Из (9): (10)

Запишем

(11)

(12)

Из (12) выразим и подставим в (11):

(13)

Из (13) выразим ускорение и приравняем к (10):

Ответ:

146. Из двух соударяющихся абсолютно упругих шаров больший шар покоится. В результате центрального упругого удара меньший шар потерял 21% своей кинетической энергии. Определить отношение масс шаров

до удара после удара

Закон сохранения импульса:

(1)

где – импульс первого тела до удара;

– импульс первого тела сразу после удара;

– импульс второго тела сразу после удара;

скорость первого тела до удара;

скорость первого тела сразу после удара;

скорость второго тела сразу после удара.

Закон сохранения энергии:

(2)

где – кинетическая энергия первого тела до удара;

– кинетическая энергия первого тела сразу после удара;

– кинетическая энергия второго тела сразу после удара.

или (3)

Преобразует (1) и (3):

(4)

(5)

Из (4) и (5) получим: (6)

Начальная кинетическая энергия первого шара: (7)

Изменение кинетической энергии первого шара:

(8)

Из (7): (9)

Из (4), (6) и (9) находим:

Ответ:

156. Человек массой 53 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 1 кг со скоростью 20 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед равен 0,02?

S = ?

Закон сохранения импульса:

(1)

где импульс конькобежца сразу после бросания;

импульс камня сразу после броска.

Из (1) начальная скорость конькобежца:

(2)

Закон сохранения энергии:

(3)

где – начальная кинетическая энергия конькобежца после броска;

– работа силы трения;

ускорение свободного падения.

Из (3) и (2) находим:

Ответ:

166. На краю свободно вращающегося горизонтального диска (радиус 3 м, момент инерции 142 кг ∙ м²) стоит человек массой 80 кг. Во сколько изменится кинетическая энергия системы , если человек перейдет от края диска к центру? Момент инерции человека рассчитать как для материальной точки.

Момент инерции человека, стоящего на краю диска:

(1)

Начальный момент инерции системы:

(2)

Начальная кинетическая энергия системы:

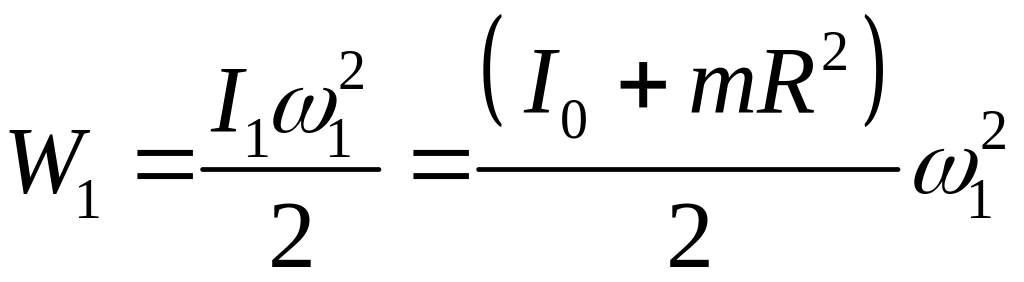(3)

где ω₁ – начальная угловая скорость вращения платформы.

Конечный момент инерции системы: (4)

Закон сохранения момента импульса:

(5)

Из (5) конечная угловая скорость платформы:

(6)

Конечная кинетическая энергия системы:

(7)

Отношение энергий:

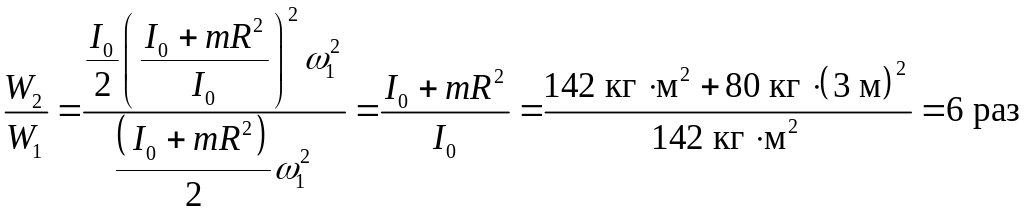
Ответ:

176. Однородный стержень массой 585 г и длиной АВ = 0,5 м может свободно вращаться вокруг горизонтальной оси , проходящей через точку О. В точку А на конце стержня попадает пластилиновый шарик, летящий горизонтально (перпендикулярно оси ) со скоростью 1 м/с и прилипает к стержню. Масса шарика 17 г. Определить линейную скорость точки В конца стержня, сразу после прилипания шарика, если расстояние АО = АВ/3.

Закон сохранения момента импульса:

(1)

где – момент импульса пластилинового шарика относительно оси z;

– момент импульса системы относительно оси z.

Момент инерции стержня относительно точки О:

(3)

Из (1) находим угловую скорость вращения, подставляя (2):

(4)

Линейная скорость точки В:

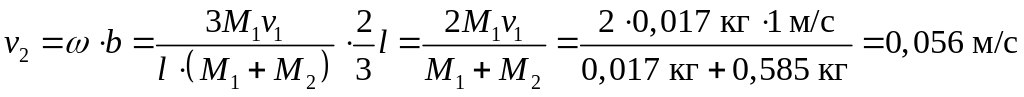
Ответ: