
Бригада_1_2020 / 2.6 Вычислительная обработка результатов измерений
.pdf
Печать
2.6 Вычислительная обработка результатов измерений
Вычислительные работы начинают с проверки полевых журналов. Суммируют значения измеренных углов и вычисляют угловую невязку.
Сумма измеренных углов,∑βизм:
изм
Теоретическую сумму углов (∑βтеор) вычислить по формуле:
теор |
; |
где n – число углов полигона. |
|
Так, для пятиугольника |
|
теор |
|
Разность между измеренной и теоретической суммой углов даст угловую невязку:
ƒ |
изм |
теор |
; |
2.6.1. Определение дирекционного угла исходной стороны (решение обратной геодезической задачи)
Для нахождения дирекционного угла исходной стороны необходимо решить обратную геодезическую задачу.
Даны координаты точек 1 (Х=30512,94 м, Y=29082,76 м) и ОР (Х=30555,60 м, Y=29083,67 м). Приращение координат находится по формуле:
Нахождение дирекционного угла зависит от того, в какой четверти находится румб, поэтому его значение находится по формуле:
/

Так как знаки приращений отрицательны, румб находится в третьей четверти, поэтому формула вычисления угла будет:
По найденному дирекционному углу и исправленным внутренним углам участка найдем угол α12
Аналогично рассчитываются остальные углы, результаты записываются в ведомость вычисления координат вершин теодолитного хода.
|
испр |
|
испр |
|
испр |
|
испр |
Контроль: |
испр |
|
2.6.2 Вычисление координат точек теодолитного ход
Вычисления координат вершин теодолитного хода производят в специальной ведомости.
Из журнала измерений горизонтальных углов заносим данные в ведомость вычисления координат вершин теодолитного хода: исходные данные, измеренные углы (примычный и горизонтальные), длины линий.
Таблица 1. Ведомость вычисления координат вершин теодолитного хода.
№ |
Горизонтальные углы |
Дирекционные |
Длины |
Приращения координат, м |
Координаты |
№ |
|
|
|
|
углы сторон |
|
|
|
|
|
/ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
вершины |
(правые по ходу, βп ) |
α |
линий |
вычисленные |
исправленные |
|
|
вершины |
|
|||
хода |
|
|
º ′ |
d, |
|
|
|
|
Х, м |
Y , м |
хода |
|
измеренные |
исправленные |
Х |
Y |
Х |
Y |
|
||||||
|
|
|||||||||||
|
º ′ |
º ′ |
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОР |
|
|
|
|
|
|
|
|
30555,60 |
29083,67 |
ОР |
|
|
|
|
181°13,3’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30512,94 |
29082,76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 (Т 1) |
221°47’ |
|
|
|
+0.01 |
+0,01 |
|
|
1 (Т1) |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
139°26,3’ |
44,04 |
- 33,46 |
28,64 |
- 33,45 |
28,65 |
|
|
|
|
|
+0,4' |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
151°2,4’ |
|
|
|
|
|
|
30479,49 |
29111,41 |
2 |
|
151°02’ |
|
|
+0.01 |
+0,01 |
|
|
|
|||||
|
|
|
168°23,9’ |
52,00 |
- 51,11 |
10,46 |
- 51,10 |
10,47 |
|
|
|
|
|
+0,4' |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
98°42,4’ |
|
|
|
|
|
|
30428,39 |
29121,88 |
3 |
|
98°42’ |
|
|
+0,01 |
+0,01 |
|
|
|
|||||
|
|
|
249°42,5’ |
52,07 |
-18,06 |
-48,84 |
-18,05 |
-48,83 |
|
|
|
|
|
+0,4' |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
92°28,4’ |
|
|
|
|
|
|
30410,34 |
29073,05 |
4 |
|
92°28’ |
|
|
|
+0,01 |
|
|
|
|||||
|
|
|
337°14,1’ |
63,23 |
58,30 |
-24,47 |
58,30 |
-24,46 |
|
|
|
|
|
+0,4' |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
5 |
|
119°36,4’ |
|
|
|
|
|
|
30468,64 |
29048,59 |
5 |
|
119°36’ |
|
|
|
+0,01 |
|
|
|
|||||
|
|
|
|
|
44,30 |
34,16 |
44,30 |
34,17 |
|
|
|
|
|
+0,4' |
|
37°37,7’ |
55,95 |
30512,94 |
29082,76 |
|
|
||||
1 (Т1) |
78°10’ |
78°10,4’ |
|
|
|
|
|
|
1 (Т1) |
|
||
139°26,3’ |
Σ267,27 |
Σ-0,03 |
Σ-0,05 |
Σ0,00 |
Σ0,00 |
|
|
|
||||
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Σβизм |
539°58’ |
540°00’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Σβт |
540°00’ |
540°00’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fβ |
-0°2’ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fβ доп |
-0°2,2’ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/
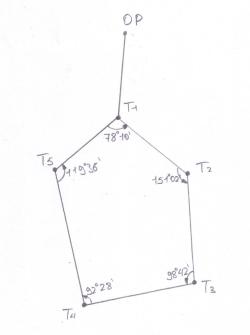
Рисунок 1 - Схема замкнутого теодолитного хода.
Угловая невязка не должна быть больше допустимой.
Допустимая невязка определяется по формуле: ƒβдоп = ±2t√n,
где ƒβдоп - предельная допустимая невязка; t - точность теодолита; n - число углов полигона.
Для пятиугольника допустимая угловая невязка будет: ƒβдоп = ±2 * 30″ * √5 = ±0°2,2′
Сравнивается фактическая угловая невязка теодолитного хода с допустимой: ƒβ ≤ ƒβдоп
-0°02′ ≤ ±0°2,2’
Если условие выполняется, то распределяют угловую невязку с обратным знаком поровну на все углы хода. Для этого вычисляем угловую поправку δβ :
δβ = -ƒβ /n |
|
где n – количество углов в полигоне. |
|
δβ = +0,4′ |
/ |

Чтобы найти координаты точек теодолитного хода, сначала нужно найти приращение координат. Для их определения воспользуемся формулами:
∆X=d∙cosα
∆Y=d∙sinα
В замкнутом полигоне суммы всех приращений координат ( в отдельности по ∆X и ∆Y) должны равняться нулю, то есть ∑X=0 и ∑Y=0. В результате ошибок измерений ∑∆X≠0 и ∑∆Y≠0 .Для получения невязок алгебраически суммируют значения ∆X и ∆Y . Результаты записывают отдельно под вычислительными приращениями.
Невязки равны:
Абсолютную величину линейной невязки вычисляем по формуле:
В нашем случае
Абсолютная невязка не характеризует точность проведённых работ. Для оценки допустимой невязки необходимо вычислить относительную невязку по формуле:
где Р – сумма длин теодолитного хода(периметр)
Р=267,29м
Относительная невязка равна:
/
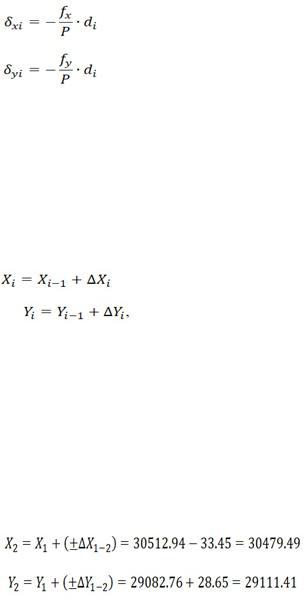
Допустимая невязка должна быть |
|
.Полученная невязка не превышает допустимой, значит распределяется в виде поправок к приращению |
|
координат. Распределение невязки производится по каждой из осей самостоятельно, пропорционально длинам сторон теодолитного хода, причем знаки поправок должны быть обратным знакам невязки. После их распределения следует сделать проверку, то есть сложить все поправки. Если их сумма будет равна невязке с обратным знаком, значит, распределение невязки выполнено правильно. Поправки выписывают над каждым приращением.
Поправки рассчитываются по формулам:
Определить величину поправки для длины линии d1-2=44,04 и невязки fx=-0.03
Аналогично вычисляем остальные поправки для приращений по оси Х и Y ,и заносим их в ведомость .
Поправки округляются до 0,01м, к вычисленным приращениям прибавляем поправки и получаем исправленные приращения, алгебраическая сумма которых равняется нулю.
По исправленным приращениям вычисляем координаты вершин полигона. Вычисляем координаты по формулам:
где Хi ,Уi – координаты последующей точки;
Хi-1, Уi-1 – координаты предыдущей точки;
х, у – приращения координат для стороны, связывающей эти точки.
Для вычисления координат необходимо знать координаты первой точки.
Условные координаты точки X1=30512,94м,Y1=29082,76м,
Следовательно:
/

Аналогично вычислить координаты для всех вершин теодолитного хода. Результаты занести в ведомость вычисления координат вершин теодолитного хода. Заключительный контроль : совпадение вычисленных координат конечной точки теодолитного хода с исходными.
Рисунок 2 - План теодолитного хода.
/
