- •«Сибирский федеральный университет»
- •Лабораторная работа №6
- •Изложить последовательность обработки результатов измерений теодолитного хода.
- •Произвести уравнивание теодолитного хода с заполнением "Ведомости вычисления координат вершин теодолитного хода".
- •Построить план теодолитного хода в масштабе 1:2 000 на листе формата а3. Построение координатной сетки
- •Контрольные вопросы
Построить план теодолитного хода в масштабе 1:2 000 на листе формата а3. Построение координатной сетки
Построение координатной сетки может быть выполнено двумя способами:
1) с помощью масштабной линейки и циркуля-измерителя;
2) с помощью линейки Дробышева.
Построение координатной сетки первым способом применяется в том случае, когда нужно вычертить координатную сетку с небольшим числом квадратов, как в нашем случае.
Вначале рассчитывают число квадратов координатной сетки по осям Х и У. Стороны квадратов координатной сетки на плане принимают равным 10 см.
Находят приращения координат:
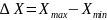 ;
;
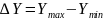 ;
;
Где
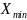 ,
,
 – минимальные значения Х
и Y,
округленные в меньшую сторону до
величины, кратной длине квадрата в
данном масштабе;
– минимальные значения Х
и Y,
округленные в меньшую сторону до
величины, кратной длине квадрата в
данном масштабе;
 и
и
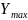 – максимальные значения X
и Y,
округленные в большую сторону до
величины, кратной длине квадрата в
данном масштабе.
– максимальные значения X
и Y,
округленные в большую сторону до
величины, кратной длине квадрата в
данном масштабе.
=2145,45
=2636,33
= 2388,78
=2947,27
Отсюда
=2000; =2400;
=2600; =3000.
Число квадратов по оси Х и Y определяется по следующим формулам:
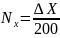 ;
;
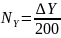 ,
где число в
знаменателе – длина стороны квадрата
в масштабе 1:2000.
,
где число в
знаменателе – длина стороны квадрата
в масштабе 1:2000.
В нашем примере:
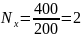 ;
;
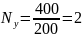 .
.
Таким образом, строим координатную сетку с числом квадратов 2х2.
Нанесение по координатам точек теодолитного хода Находим квадрат, в котором лежит данная точка. Например, точка 1 по исходным данным имеет координаты:
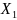 =
2145,45 м;
=
2145,45 м;
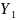 =2827,13
м.
=2827,13
м.
Она лежит в квадрате, координаты юго-западного угла которого 2000 и 28000.
Найдём приращение координат этой точки над координатами юго-западного угла:
△Х = 2145,45 – 2000 = 145,45 м;
△Y = 2827,13 – 2800 = 27,13 м.
Выражая отрезки △Х и △Y в масштабе плана и откладывая их по соответствующим осям квадрата, строим точку 1. Аналогично на план наносим и другие вершины теодолитного хода. После нанесения и нумерации теодолитного хода соединяем их прямыми линиями, подписываем дирекционные углы и длины линий.
Правильность нанесения вершин теодолитного хода проверяют:
По длинам сторон теодолитного хода (допустимое расхождение не более 0,4 мм);
По дирекционным углам сторон;
По внутренним углам при вершинах теодолитного хода.
Вокруг всего плана вычерчивают рамку. Внизу под рамкой подписывают масштаб, и кто выполнил работу.
Контрольные вопросы
Что называется погрешностью измерения? Что такое грубые, систематические и случайные погрешности измерений?
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Грубые погрешности существенно превышают погрешности, оправданные условиями измерения, свойствами примененных средств измерений, методом измерений и квалификацией экспериментатора.
Систематические - это погрешности постоянные или закономерно изменяющиеся при повторных измерениях одной и той же величины.
Случайными называются погрешности, неопределенные по своей величине или не достаточно изученные, в появлении значений которых не удалось установить какой-либо закономерности.