Федеральное государственное автономное

образовательное учреждение

высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

САЯНО-ШУШЕНСКИЙ ФИЛИАЛ

Кафедра фундаментальной подготовки

Расчетно-графическое задание

по математике (семестр 2)

Преподаватель ________ О.В. Кравцова

подпись, дата инициалы, фамилия

Студент ГЭ20-02Б ________ М.Д.Кобзарь

номер группы, зачетной книжки подпись, дата инициалы, фамилия

Черемушки, 2021

№17.30 Материальная точка движется по закону , где – время, x – координата точки. График гладкой функции образован отрезком прямой AB и двумя дугами парабол OA и BC. \

A(4,9) B(8,1) C(12,11)

1. Составить формулу, задающую функцию .

2. Найти скорость точки и ее ускорение .

3. Построить графики функций , , .

4. Указать наибольшую и наименьшую скорость точки при .

Решение:

Так как функция является гладкой на интервале, то ее производная на этом интервале является непрерывной.

Составим уравнение прямой, проходящей через точки A(4;9) и B(8;1):

Окончательно получаем:

Так как для функция является квадратичной, запишем ее в виде . Поскольку парабола проходит через точку , то с = 0.

Из условия непрерывности функции в точке имеем:

По условию гладкости приравниваем производные функции в этой точке: или

Получим систему уравнений:

Откуда: ,

Таким образом, при получили: .

Аналогично для участка параболы, соединяющей точки B(8;1) и C(12;11), представим функцию а виде и запишем условия:

,

Получим систему уравнений:

Решение которой: , , .

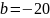Таким образом, при получили

Окончательно запишем кусочно-заданную функцию:

Построим ее график:

Дифференцируя найденную функцию, найдем скорость и ускорение :

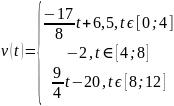
Построим графики функций:

Найдем наибольшее и наименьшее значения функции на отрезке . Так как функция кусочно-линейная, то исследование на экстремум с помощью производной не требуется:

№8.30 Даны результаты 10 измерений некоторой величины При помощи метода наименьших квадратов найти функцию, приближенно принимающую таблицу значений,

1. Линейную ,

2. Квадратичную ,

Так, чтобы сумма квадратов погрешностей была минимальной. Сделать чертеж.

Исходные данные:

хi	-8	-7	-6	-5	-4	-3	-2	-1	0	1
yi	3,0	1,1	-0,6	-1,2	-0,4	2,0	3,0	6,5	12,1	17,9

Решение:

1) Для определения линейной функции составим систему уравнений, которая имеет вид:

Составим промежуточную таблицу для расчетов:

n	х	у	х2	y∙x	улин
1	-8	3,0	64	-24,0	-2,79
2	-7	1,1	49	-7,7	-1,21
3	-6	-0,6	36	3,6	0,38
4	-5	-1,2	25	6,0	1,96
5	-4	-0,4	16	1,6	3,55
6	-3	2,0	9	-6,0	5,13
7	-2	3,0	4	-6,0	6,72
8	-1	6,5	1	-6,5	8,30
9	0	12,1	0	0,0	9,89
10	1	17,9	1	17,9	17,47
Сумма	-35	43,4	205	-21,1

Подставляем в систему полученные в таблице значения:

Решая систему уравнений, находим: .

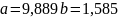Линейная функция имеет вид: