9. Кривая обеспеченности расхода (стока).

Кривая обеспеч.- кривая, хар-ая вероятность достижения/превышения гидрол. величины.

Теор. кривые обеспче. в гидрологии наиб. часто исп-ся для опред-ия ср.год. значения стока, мах. и мин.. расходов.

Аналитическая кривая строиться с помощью специальных таблиц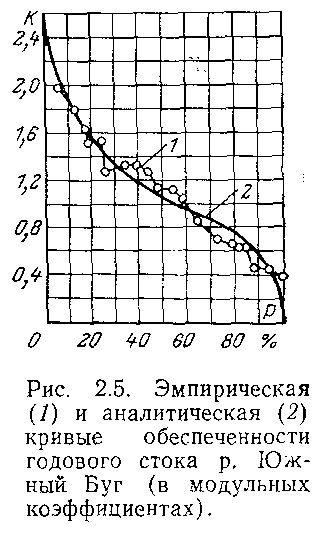 ординат кривых обеспеченности (разных для различных распределений). Для распределения Пирсона III (бинормальная кривая распред) типа Фостером и Рыбкиным, а для трехпараметрического гамма-распределения С.Н.Крицким и М.Ф.Менкелем. При этом исп-ся следующие параметры кривой обеспеченности:

Средний расход реки: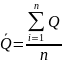

Где n – объем выборки.

Коэффициент вариации:

Коэффициент асимметрии:

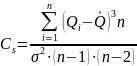
Где – среднеквадратичное отклонение:

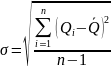
Для кривой Пирсона:

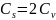
10. Алгоритм построения эмпирической кривой обеспеченности расхода

Эмпирическая кривая строится с помощью ряда наблюдений расположенному в порядке убывания и каждому его значению соответствует вероятность, вычисленная по формуле:

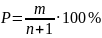
n – объём выборки; m – порядковый номер данного члена в убывающем ряду.

1. Расположить расходы в порядке убывания

2. Вычислить среднемноголетний расход

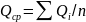
3. Вычислить модульный коэффициент .(В сумме общ. число n)

4. Вычислить отклонение от середины:

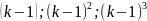
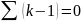
5. Рассчитать коэф. вариации:

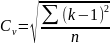
6. Рассчитать коэф асимметрии:

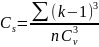
7. Ср квадр. ошибка вариации:

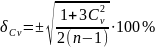
8. Среднеквадратическая ошибка асимметрии: 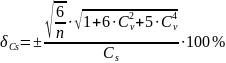если данная ошибка получается выше среднего то принимаем

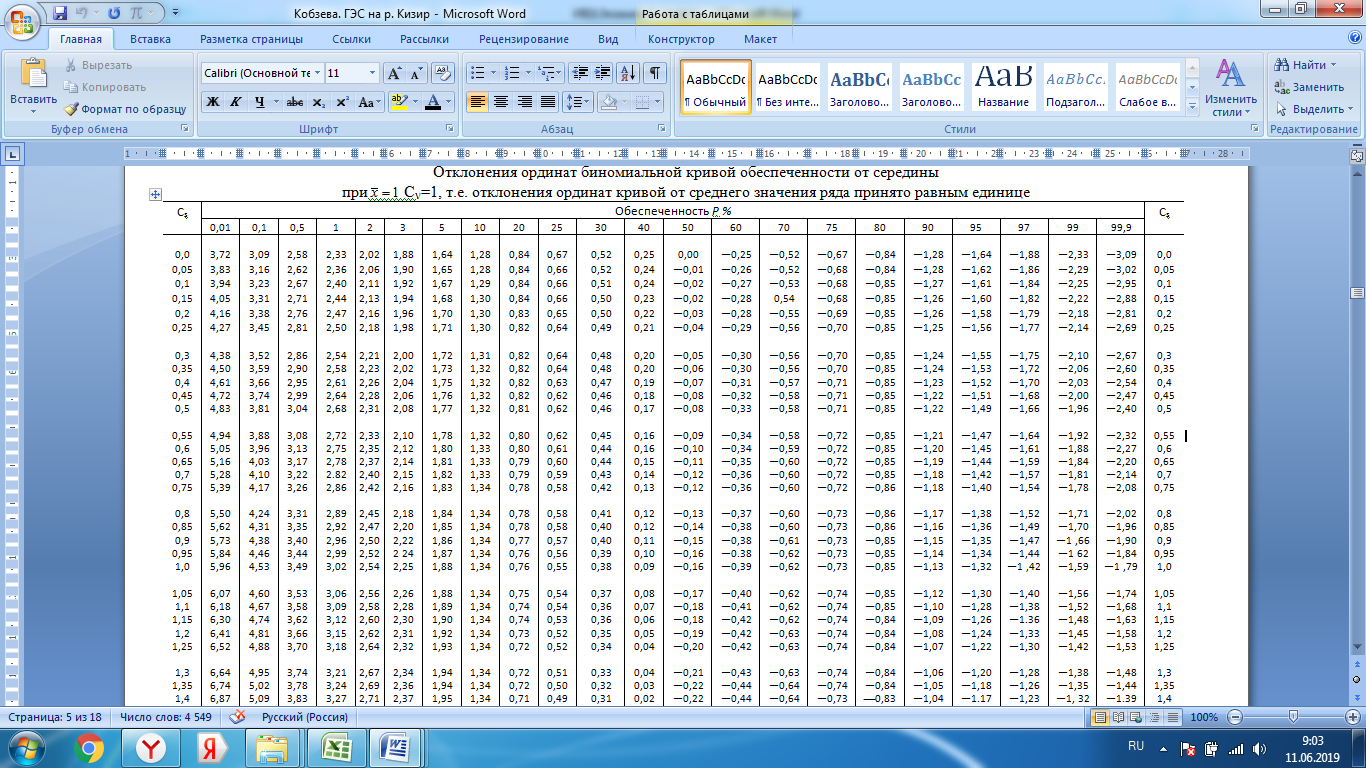
9. Зная величины параметров Q_ср, C_v и C_s, вычисление теоретической кривой обеспеченности средних годовых расходов производят по таблице С.И. Рыбкина – П.А. Алексеева , в к-й даны относ. отклонения от середины ординат интегральной кривой при С_v = 1,00 и разных процентах обеспеченности P.

11. Теоретические кривые распределения вероятностей в гидрологических расчетах

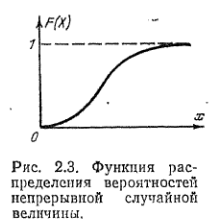
Е сть несколько теор. кривых распред. вероятностей, наиб. употребительными являются двух- (кривая Пирсона III типа) и трехпараметрическое(распределение Крицкого-Менкеля) гамма-распределения. Приминая в качестве верхней границы +∞, считают, что такое событие имеет практически нулевую вероятность. Принимая в качестве нижней границы речного стока нуль, предполагают, что в реальных реках гидрологические характеристики никогда не снижаются до 0 (Появление нуля в качестве нижней границы рассматривается как чрезвычайно маловероятное событие, равное абсолютному пределу снижения расходов воды в реке).

Производная функции распределения характеризует плотность. С которой распределяются значения случайной величины в данной точке, и называется плотностью распределения (плотностью вероятности).

Кривая, изображающая плотность распределения, называется кривой распределения.

Кривая обеспеченности – интегральные выражения для распределений; зависимости между величинами и вероятностью их достижения или превышения.

1) Теоретическая (аналитическая) кривая строится с помощью спец таблиц ординат кривых обеспеченности (Рыбкин)

2) Эмпирическая кривая обеспеченности для построения которой ряд располагают в убывающем порядке и каждому его значению приписывается опред. вероятность превышения в соответствии с формулой

Для удобства работы разработаны спец логарифмические сетки координат – клетчатки вероятности. Теоретическая кривая обеспеченности на такой клетчатке превращается в прямую или слабо искривленную линию.

На практике получила широкое распространение клетчатка вероятностей Хазена, которая линеаризует распределение, оставляя при этом масштаб по оси рассматриваемых случайных величин.