ргз2-1
.docxФедеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Саяно-Шушенский филиал
институт
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №2
по Гидромеханике
предмет
Гидравлический расчет трапецеидального канала при неравномерном движении
тема
Вариант № 4.4
Преподаватель _________________ А.А.Андрияс
подпись, дата
Студент гр. СБ19-01Б _________________ Д.В.Нефедов
подпись, дата
рп. Черёмушки, 2021
Цель: требуется определить тип кривой свободной поверхности на участке от ПК0 до ПКn при пропуске нормального расхода Q. Построить продольный профиль трапецеидального канала.
Состав расчёта: определить тип кривой свободной поверхности на участке канала отПК0 до ПКn при пропуске нормального расхода Q.
Построить продольный профиль трапецеидального канала с участком неравномерного движения в масштабах МГ 1:10; МВ 1:10000.
Исходные данные:
Таблица 1 – Исходные данные для выполнения расчётно-графического задания
Вариант |
Исходные данные |
||||||
Нормальная глубина
|
Ширина канала по дну
|
|
|
Уклон канала |
Глубина воды
|
Номер пикетаПКn |
|
4 |
3,0 |
6,0 |
2,0 |
0,04 |
0,35 |
0,6* |
53 |
Расход воды в канале равен номеру варианта Q=44 м^3/с.
Критическую глубину канала hKP в трапецеидальном русле будем определять по методу И.И. Агроскина:

где,
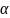 – коэффициент Кориолиса, связанный с
неравномерностью распределения скоростей
по сечению и принимаемый
– коэффициент Кориолиса, связанный с
неравномерностью распределения скоростей
по сечению и принимаемый ;
;
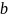 – ширина канала по дну м;
– ширина канала по дну м;
 – расчётный расход канала,
– расчётный расход канала, ;
;
 – ускорение свободного падения,
– ускорение свободного падения, .
.
Далее определяется параметр
 :
:

где, – коэффициент откоса данного канала.
Далее, пользуясь справочной таблицей
определяется значение функции
 составленной
И.И. Агроскиным, и вычисляем искомую
критическую
глубину
данного трапецеидального канала.
составленной
И.И. Агроскиным, и вычисляем искомую
критическую
глубину
данного трапецеидального канала.
По таблице “Числовые значения функции
для определения критической глубины
трапецеидального канала” было выяснено,
что при значении
 ,
,
 .
.
Далее рассчитываем глубину трапецеидального канала:

Рассчитаем критический уклон:

Но для подсчёта критического уклона для начала необходимо узнать следующие величины:



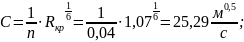

В открытых призматических руслах при неравномерном движении, в зависимости от величины уклона дна и условий протекания потока в начале и в конце рассматриваемого участка, может образовываться ряд форм свободной поверхности потока.
На данном этапе определяем, какого типа
будет кривая свободной поверхности.
Чтобы это сделать, будет достаточно
сравнить следующие величины: уклон
канала
 и критический уклон канала
и критический уклон канала
 ,
а также величины глубин: нормальной
глубины
,
критической глубины
,
а также величины глубин: нормальной
глубины
,
критической глубины и глубины воды
на ПК0.
и глубины воды
на ПК0.
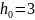 – нормальная глубина канала,
;
– нормальная глубина канала,
;
 – критическая глубина канала,
;
– критическая глубина канала,
;
 – глубина канала на нулевом пикете,
;
– глубина канала на нулевом пикете,
;
При прямом уклоне дна i > 0
Первый случай
Если уклон дна русла i меньше критического уклона iKP (i < iKP), т.е. глубина равномерного движения потока h0 больше критической глубины hKP (h0 > hKP), существуют три вида кривых свободной поверхности: в зоне а – кивая подпора а1 в зоне b – кривая спада b1 в зоне с – кривая подпора – c1 (рисунок 1).

Рисунок 1 – Кривые свободной поверхности при h0>hкр
Исходя из анализа вышеприведённых данных делаем вывод, что у нас получается кривая подпора типа b1.
Метод Б.А. Бахметева
Расстояние между сечениями с глубинами h1 и h2 для случая i > 0 определяется по формуле:

где l1-2 – расстояние между сечениями с глубинами h1 и h2, м;
h0 – глубина равномерного движения, м;
1, 2 – относительные глубины, м:

(1), (2) – функции Бахметева. Функции (1), (2) определяются по таблицам Приложения 3 в зависимости от значения относительной глубины i и гидравлического показателя русла X.
Гидравлический показатель русла определяется по зависимости:

где K1 и K2 – расходные характеристики для первого и второго створов на рассматриваемом участке канала, соответствующие глубинам h1 и h2.
Скоростной коэффициент j находится по формуле:

где – коэффициент, учитывающий неравномерность распределения скоростей по живому сечению потока;
С – коэффициент Шези, м0,5/с;
B – ширина канала по урезу воды, м;
χ – смоченный периметр, м.
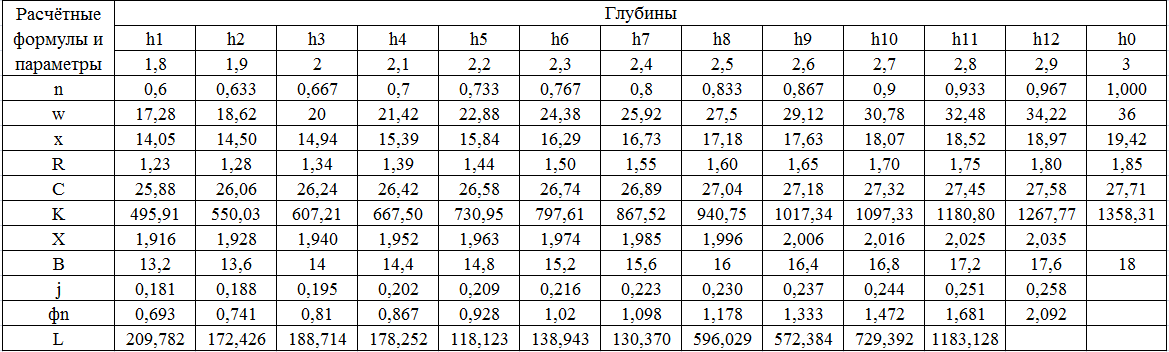
Расчет кривой свободной поверхности методом Б.А. Бахметева удобно вести в табличной форме (таблица 2).
Таблица 2 – Расчёт кривой свободной поверхности по методу Б.А. Бахметева










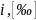
 на
ПК0,
на
ПК0,