РГЗ
.docxМинистерство науки и высшего образования РФ
Федеральное государственное автономное
Образовательное учреждение высшего образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Саяно-Шушенский филиал
институт
РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №4
по Гидравлике
наименование дисциплины
Расчет трубопровода
тема работы
Схема 3
Вариант 5
Преподаватель __________ А.А.Андрияс
инциалы фамилия
Студент ГЭ 17-02Б 1721553 __________ Д.С. Глашев
номер группы зачетной книжки подпись, дата инциалы фамилия
Черемушки 2018
Цель: выполнить гидравлический расчет трубопровода переменного или постоянного сечения, по которому жидкость подается из резервуара.
Задачи:
1. Определить скорости стечения жидкости, расход и потери напора предполагая наличие турбулентного режима движения.
2. Выполнить проверку точности результатов расчета.
3. Уточнить режим движения жидкости в трубе при заданном коэффициенте кинематической вязкости.
4. Построить в масштабе линии полного и пьезометрического напора.
Исходные данные:
Н, м |
ρ,кг/м3 |
|
|
l1,м
|
d1,мм
|
l2,м
|
d2,мм
|
|
𝜆
|
ν, м2/с
|
4
|
900
|
3 |
1 |
5
|
25
|
2
|
32
|
1,8
|
0,02
|
30*10-6
|
Решение:
1.Определить скорость истечения, расход, потери напора, предполагая наличие турбулентного режима движения.
Расчет производится по следующей схеме:
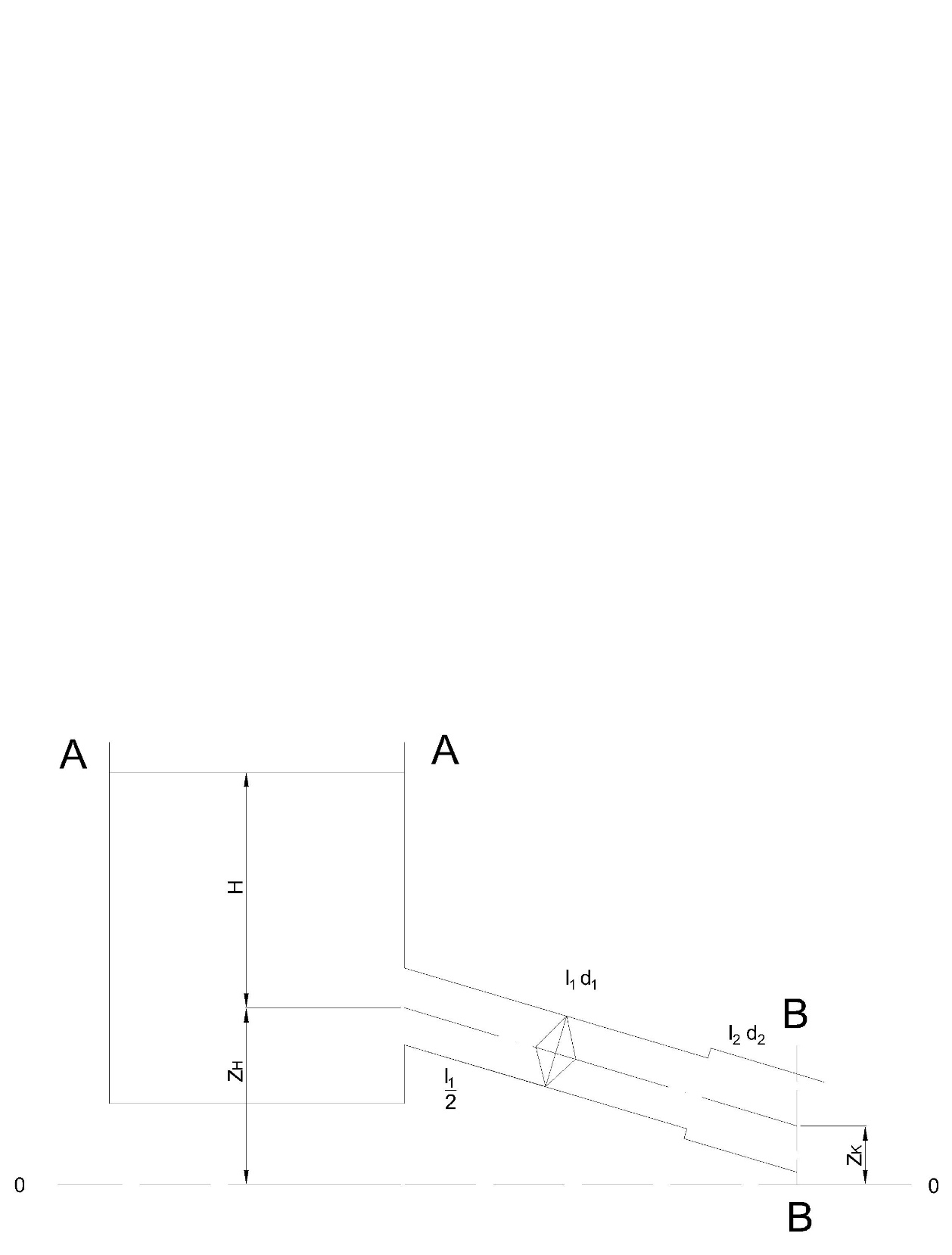
Рисунок 1- Исходная схема 3
Запишем уравнение Бернулли для сечения А-А и В-В.
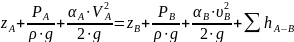 (1.1)
(1.1)
Где:

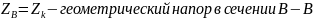
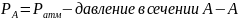

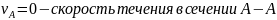
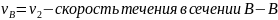
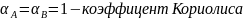
После подстановки значений в уравнение Бернулли, оно примет следующий вид:
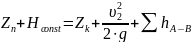 (1.2)
(1.2)
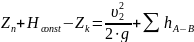 (1.3)
(1.3)
Так как заданный трубопровод состоит из двух последовательно соединенных труб, то общие потери определяются как сумма всех потерь
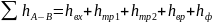
Используя формулы Дарси и Вейсбаха найдем:
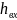 =
=
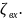
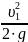
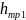 =
=
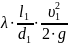
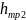 =
=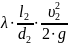
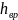 =
=

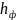 =
=
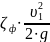
Где:
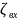 =
0,5 по условию задания
=
0,5 по условию задания
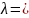 ..0,03),
примем равным 0,02
..0,03),
примем равным 0,02
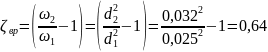
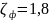 по
условию задания
по
условию задания
Изменим формулу (1.3) для удобства таким образом:
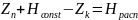 (1.4)
(1.4)
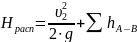 (1.5)
(1.5)
Где
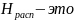 располагаемый
напор, затрачиваемый на преодоление
всех сопротивлений и создания скорости
располагаемый
напор, затрачиваемый на преодоление
всех сопротивлений и создания скорости
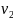 на выходе из трубы.
на выходе из трубы.
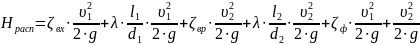 (1.6)
(1.6)
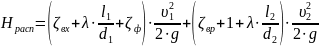 (1.7)
(1.7)
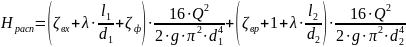 (1.8)
(1.8)
Выразим и посчитаем расход:
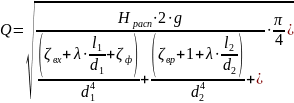 (1.9)
(1.9)
Где:
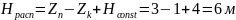
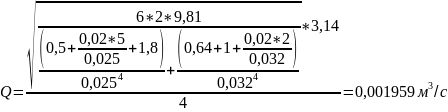
Выразим
и посчитаем скорость
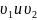 :
:
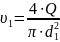 (2.0)
(2.0)
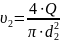 (2.1)
(2.1)
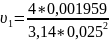 =
3,993
м/c
=
3,993
м/c
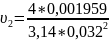 =
2,437
м/c
=
2,437
м/c
2.Выполнить проверку точности результатов расчета подставив полученные скорости.
(2.2)
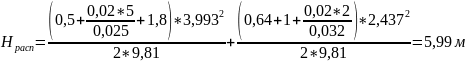
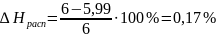 (2.3)
(2.3)
3.Уточнить режим движения жидкости в трубе при заданном коэффициенте кинематической вязкости.
Рассчитаем критерий Рейнольдса:
Для первой трубы:
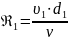 (2.4)
(2.4)
Где:
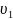 -
скорость
жидкости в первом участке трубы.
-
скорость
жидкости в первом участке трубы.
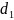 -
диаметр первого участка трубы.
-
диаметр первого участка трубы.
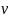 – коэффициент
кинематической вязкости.
– коэффициент
кинематической вязкости.
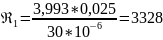
 ,
значит, найдем коэффициент гидравлического
трения по формуле Блазиуса:
,
значит, найдем коэффициент гидравлического
трения по формуле Блазиуса:
Для этого рассчитаем для первого участка трубы
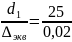 =
1250
=
1250
Если критерий Рейнольдса попадает в интервал, то поверхность гидравлически гладкая. Проверим выполнение условия:
2320
<
 < 10
< 10 (2.5)
(2.5)
2320 < < 12500 – условие выполняется, значит, поверхность гидравлически гладкая.
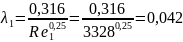 (2.6)
(2.6)
Для второй трубы:
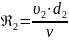 (2.7)
(2.7)
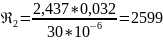
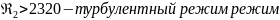 ,
значит, найдем коэффициент гидравлического
трения по формуле Блазиуса:
,
значит, найдем коэффициент гидравлического
трения по формуле Блазиуса:
Для этого рассчитаем для второго участка трубы:
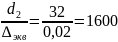 (2.8)
(2.8)
Если критерий Рейнольдса попадает в интервал, то поверхность гидравлически гладкая. Проверим выполнение условия:
2320
<
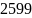 < 10
< 10
2320 < < 16000 – условие выполняется, значит, поверхность гидравлически гладкая.
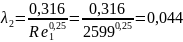
Пересчитаем расход и скорости с новыми коэффициентами λ :

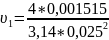 =3,088
м/c
=3,088
м/c
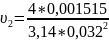 =
1,885
м/c
=
1,885
м/c
4.Построить в масштабе линию полного и пьезометрического напора.
Перед построением необходимо выполнить проверку:
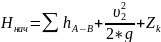 ,
(2.9)
,
(2.9)
Где
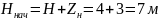 – начальный напор.
– начальный напор.
Рассчитаем потери напора:
=
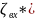
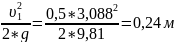 (3.0)
(3.0)
=
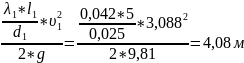 (3.1)
(3.1)
=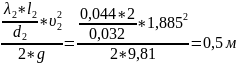 (3.2)
(3.2)
=
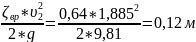 (3.3)
(3.3)
=
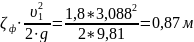 (3.4)
(3.4)
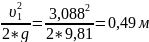
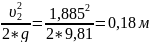
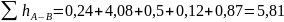 м
м
Проверка:
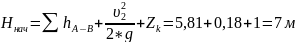
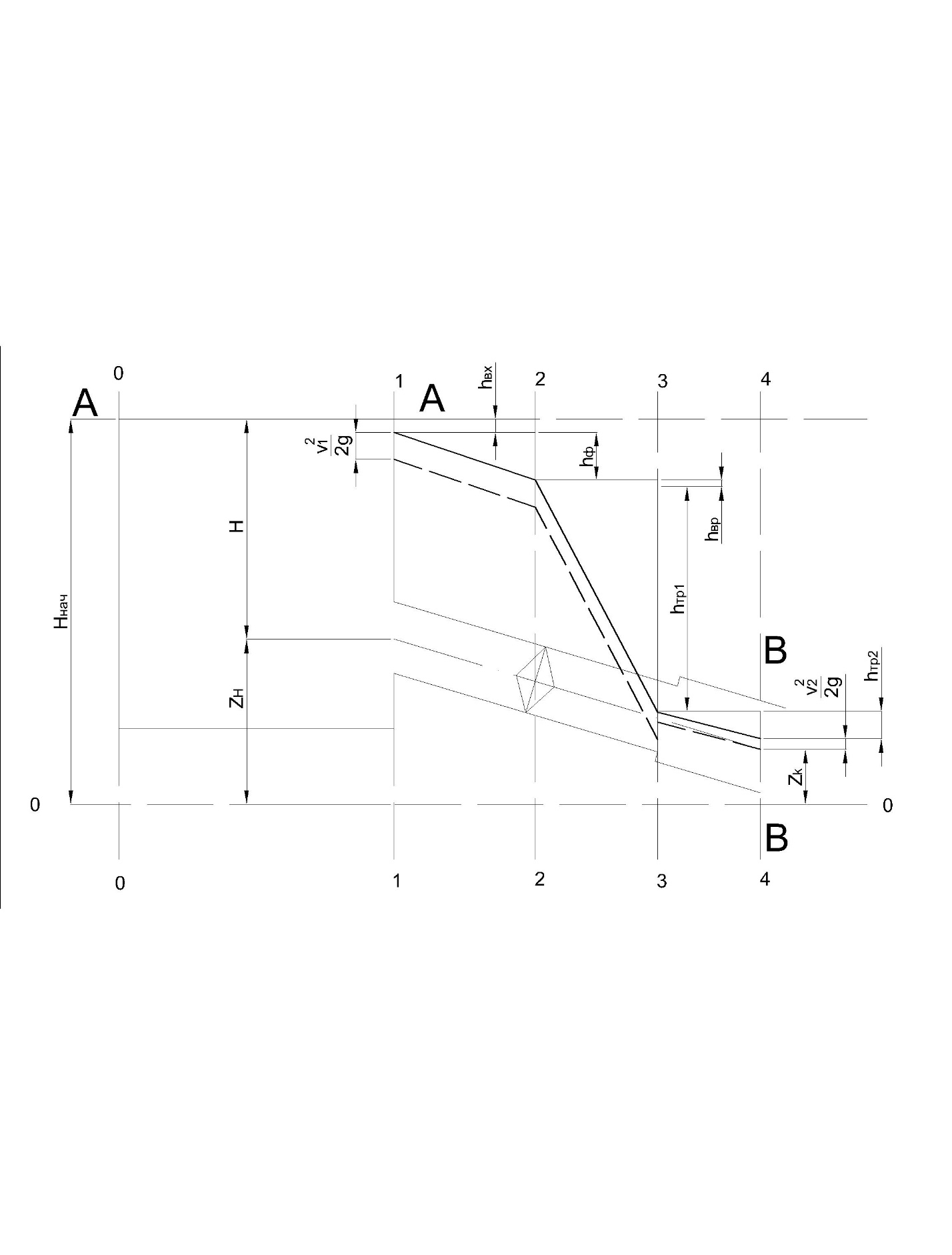
Рисунок 2 – Линии полного и пьезометрического напора

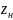 ,
м
,
м ,
м
,
м