
РГЗ 6, 37 вариант
.docxФедеральное государственное автономное
образовательное учреждение
высшего образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Саяно-Шушенский филиал
Расчетного графическое задание – 6
“ РАСЧЕТ РАЗВЕТВЛЕННОЙ МАГНИТНОЙ ЦЕПИ ”
Вариант 37
Преподаватель В.Ю. Ельникова
подпись, дата
Студент ГЭ16-03Б Мироненко Е.П.
номер группы подпись, дата
рп. Черемушки
2018г
Рассчитаем разветвленную магнитную цепь (рис. 1)

Рис.1
Дано:
 А;
А;
 А;
А; витков;
витков;
 витков;
витков;
 см;
см;
 см;
см;
 см;
см;
 см;
см;
 см2.
см2.
Основная кривая намагничивания B(H) листовой стали магнитопровода приведена в табл. 1.
Таблица 1
H, А/м |
0 |
200 |
230 |
300 |
400 |
500 |
670 |
900 |
1200 |
1600 |
B, Тл |
0 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
H, А/м |
2250 |
3200 |
4700 |
8000 |
13000 |
B, Тл |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
Требуется определить магнитные потоки Ф1, Ф2, Ф3 в стержнях; магнитную индукцию В0 в воздушном зазоре; магнитные сопротивления RM участков цепи; индуктивности L1 и L2 катушек.
Решение:
1. Узловые точки магнитной цепи обозначим буквами a и b.
2. По заданным направлениям токов I1, I2 и направлениям намотки витков катушек определяем направления МДС по правилу правого винта (или с помощью мнемонического правила: если сердечник мысленно охватить правой рукой, расположив пальцы по току в обмотке, по отогнутый большой палец укажет направление МДС).
МДС F1 и F2 направлены вверх (к узлу a), и равны:
 А;
А;
 А.
А.
Искомые магнитные потоки Ф1 и Ф2 направляем по соответствующим МДС (к узлу a), а искомый поток Ф3 в стержне, не содержащем МДС, – от узла a (см. рис. 2).

Рис.2
3. Пренебрегая потоками рассеяния, записываем для заданной магнитной цепи уравнения по законам Кирхгофа:

Падение магнитного напряжения на первом стержне:
 .
.
Падение магнитного напряжения на втором стержне:
 .
.
Падение магнитного напряжения на третьем стержне:

С учетом этого получаем систему уравнений по законам Кирхгофа в виде:

4. Пользуясь формальной аналогией между магнитными и электрическими цепями, изображаем для заданной магнитной цепи электрическую схему замещения.
Наличие воздушного зазора во втором стержне магнитопровода учитываем введением во вторую ветвь схемы замещения линейного сопротивления R0 (рис. 3).

Рис.3
5. К полученной нелинейной электрической цепи применяем метод двух узлов. Магнитное напряжение между узлами a и b обозначим UМab.
Запишем уравнения по второму закону Кирхгофа, связывающие падения магнитного напряжения на участках цепи, магнитное напряжение между двумя узлами UМab и МДС в ветвях:
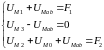
Из этих уравнений выразим магнитное напряжение UМab между узлами цепи через падение магнитного напряжения и МДС для каждого стержня магнитопровода:
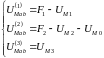
6.Задаваясь значениями магнитной индукции B, находим соответствующие им значения:
– напряженности магнитного поля H;
– магнитного потока Ф = В∙S;
– напряженности поля в воздушном зазоре H 0 = 0,8 106 В;
– падений магнитного напряжения на участках магнитопровода;
– магнитного напряжения UМab между узлами цепи для каждого стержня.
Результаты расчетов сводим в таблицу.
Таблица 2
B, Тл |
H, А/м |
Ф, Вб |
H0, А/м |
UM1, А/м |
UM2, А/м |
UM3, А/м |
UM0, А/м |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2400 |
1600 |
0 |
0,5 |
200 |
0,00075 |
400000 |
70 |
70 |
32 |
800 |
2330 |
730 |
32 |
0,6 |
230 |
0,0009 |
480000 |
80,5 |
80,5 |
36,8 |
960 |
2319,5 |
559,5 |
36,8 |
0,7 |
300 |
0,00105 |
560000 |
105 |
105 |
48 |
1120 |
2295 |
375 |
48 |
0,8 |
400 |
0,0012 |
640000 |
140 |
140 |
64 |
1280 |
2260 |
180 |
64 |
0,9 |
500 |
0,00135 |
720000 |
175 |
175 |
80 |
1440 |
2225 |
-15 |
80 |
1 |
670 |
0,0015 |
800000 |
234,5 |
234,5 |
107,2 |
1600 |
2165,5 |
-234,5 |
107,2 |
1,1 |
900 |
0,00165 |
880000 |
315 |
315 |
144 |
1760 |
2085 |
-475 |
144 |
1,2 |
1200 |
0,0018 |
960000 |
420 |
420 |
192 |
1920 |
1980 |
-740 |
192 |
1,3 |
1600 |
0,00195 |
1040000 |
560 |
560 |
256 |
2080 |
1840 |
-1040 |
256 |
1,4 |
2250 |
0,0021 |
1120000 |
787,5 |
787,5 |
360 |
2240 |
1612,5 |
-1427,5 |
360 |
1,5 |
3200 |
0,00225 |
1200000 |
1120 |
1120 |
512 |
2400 |
1280 |
-1920 |
512 |
1,6 |
4700 |
0,0024 |
1280000 |
1645 |
1645 |
752 |
2560 |
755 |
-2605 |
752 |
1,7 |
8000 |
0,00255 |
1360000 |
2800 |
2800 |
1280 |
2720 |
-400 |
-3920 |
1280 |
1,8 |
13000 |
0,0027 |
1440000 |
4550 |
4550 |
2080 |
2880 |
-2150 |
-5830 |
2080 |
7. По данным табл. 2 строим вебер-амперные характеристики Фk(UMab) стержней магнитопровода (Приложение 1).
Искомое магнитное напряжение UMab определяется режимом, где выполняется первый закон Кирхгофа. В рассматриваемом примере имеем Ф1 + Ф2 = Ф3 . Исходя из этого, строим дополнительную кривую Ф1 + Ф2 = f(UMab), суммируя потоки Ф1 и Ф2 при произвольно выбранных значениях UMab.
По данным табл. 2 строим вебер-амперные характеристики.
(Приложение 1)
Точка пересечения характеристики Ф3(UМab) с Ф1 + Ф2 = f(UМab) соответствует действительному значению магнитного напряжения UМab и дает искомые значения магнитных потоков Ф1 , Ф2 и Ф3
 Вб;
Вб;
 Вб;
Вб;
 Вб
Вб
Проверяем найденные величины потоков, подставив их значения в уравнение по первому закону Кирхгофа:

8. По найденным потокам Ф1, Ф2 и Ф3 можно определить индукции В1, В2 и В3 в стержнях магнитопровода, а по индукциям и ОКН (Приложение 2)– напряженности магнитного поля H1, H2 и H3:
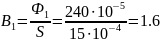 Тл,
Тл,
 А/м;
А/м;
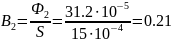 Тл,
Тл,
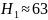 А/м;
А/м;
 Тл,
Тл,
 А/м.
А/м.
Если пренебречь боковым распором силовых линий в воздушном зазоре и считать, что сечение магнитного потока в нем равно сечению стержня магнитопровода S0 = S1 = S, то магнитная индукция в воздушном зазоре В0 = В2 = 0,21 Тл.
9. По найденным значениям В и Н рассчитываем абсолютную магнитную проницаемость соответствующих стержней:
 Гн/м;
Гн/м;
 Гн/м;
Гн/м;
 Гн/м.
Гн/м.
10. Зная магнитную проницаемость, находим магнитные сопротивления всех участков магнитной цепи:
 Гн-1;
Гн-1;
 Гн-1;
Гн-1;
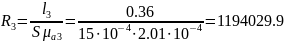 Гн
Гн-1;
Гн
Гн-1;
 Гн-1;
Гн-1;
11.
Так как потокосцепление катушки
Ф·w
L·I
, то ее индуктивность
 .
Зная магнитные потоки Ф1
и Ф2
, определяем индуктивности катушек:
.
Зная магнитные потоки Ф1
и Ф2
, определяем индуктивности катушек:
 Гн;
Гн;
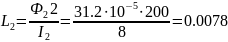 Гн.
Гн.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демирчян К.С., Л.Р. Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники: учебник для вузов: в 2 т. – М.; СПб.: Питер, 2009.
2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: учебник для бакалавров. – М.: Юрайт, 2016.
3. Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи: учебник. – М.; СПб.: Лань. 2010.
4. Ельникова В.Ю., Кочетков В.П. Теоретические основы электротехник. В 2-х частях. Часть 2. Электрические цепи: Учебное пособие. – Абакан: ООО «Фирма «Март», 2003

 ,
А/м
,
А/м ,
А/м
,
А/м ,
А/м
,
А/м