
РГЗ 5, 32 схема
.docxФедеральное государственное автономное
образовательное учреждение
высшего образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Саяно-Шушенский филиал
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №5.2
Расчёт цепей 2-го порядка классическим методом
Вариант № 32
Преподаватель __________ В.Ю.Ельникова
подпись, дата
Студент ГЭ17-02Б 1721549 __________ Д.А.Артюх
номер группы номер зачетной книжки подпись, дата
п. Черёмушки, 2019
Содержание
Исходные данные 3
Требуется 3
Ход работы 4
1. Момент до коммутации t(0-). 4
2. Момент после коммутации t(0+) 4
3. Установившейся процесс в цепи после коммутации t(∞) 5
4. Нахождение корней характеристического уравнения 6
5. Составление функций iL(t) и uC(t) 7
6. Графики функций iL(t) и uC(t) 8
Cписок используемых источников 10
Основная литература 10
Дополнительная литература 10
Исходные данные
Дана электрическая цепь второго порядка, в которой происходит коммутация. В цепи действует постоянная ЭДС. Схема исследуемой цепи представлена на рисунке 5.1 (E = U):

Рисунок 5.1 – Исходная схема цепи
Исходные параметры цепи приведены в таблице 5.1
Таблица 5.1 – Параметры цепи
Вариант |
Схема |
U , B |
|
|
|
L , Ф |
C , Ф |
32 |
5.2.2 |
100 |
30 |
10 |
10 |
0,01 |
0,0001 |
Требуется
Рассчитать переходный процесс в цепи и определить закон изменения во времени тока в ветви с индуктивностью iL(t) и напряжения на ёмкости uC(t). Построить графики iL(t) и uC(t)
Ход работы
Момент до коммутации t(0-).
Схема до коммутации цепи представлена на рисунке 5.2

Рисунок 5.2 – Схема в момент до коммутации
При постоянном воздействии в электрической цепи на конденсаторе возникает разрыв цепи, а катушка закорачивается.


Момент после коммутации t(0+)
В момент замыкания ключа схема, представленная на рис. 5.1, преобразуется в схему, представленную ниже (рис. 5.3):

Рисунок 5.3 – Схема в момент после коммутации
В соответствии с первым законом коммутации:
=> Разрыв
В соответствии со вторым законом коммутации:
Для расчета неизвестных в пункте 5 рассчитаем производные функций тока в ветви с катушкой индуктивности и напряжения на конденсаторе в начальный момент времени. Для этого найдем токи в цепи методом контурных токов:




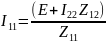

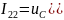





Установившейся процесс в цепи после коммутации t(∞)
Преобразованная схема представлена на рисунке 5.4:

Рисунок 5.4 – Схема в установившемся режиме после коммутации


Нахождение корней характеристического уравнения
Для решения данных уравнений, необходимо найти корни характеристического уравнения, которое составляется с условием входного напряжения в уже установившемся режиме после коммутации (рис. 5.5)
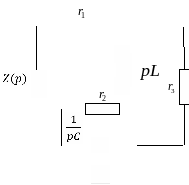
Рисунок 5.5 – Входное сопротивление
Составим уравнение для входного сопротивления и приравняем его к 0:







Корни отрицательные равные => критический процесс
Составление функций iL(t) и uC(t)
Уравнение для тока через ветвь с катушкой:

Найдем постоянную интегрирования А и
начальную фазу
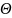 из начальных условий:
из начальных условий:






Уравнение для напряжения на конденсаторе:

Найдем постоянную интегрирования А и начальную фазу из начальных условий:






Рассчитаем время переходного процесса:

Графики функций iL(t) и uC(t)
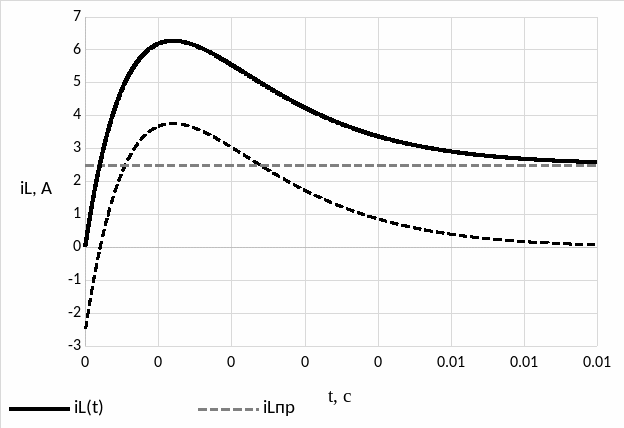
Рисунок 5.6 – график функции iL(t)

Рисунок 5.7 – График функции uC(t)
Cписок используемых источников
Основная литература
Л.А.Бессонов Теоретические основы электротехники. М.: Высшая школа, 2000
Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов Основы теории цепей.
М.: Энергоатомиздат, 1989
3. К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л.Чечурин Теоретические основы электротехники, т.1,2 – СПб.: Питер, 2004
4. А.И. Инкин Электромагнитные поля и параметры электрических машин,
учебное пособие. Н.: ЮКЭА, 2002
5. Сборник задач и упражнений по теоретическим основам электротехники,
под ред. П.А.Ионкина. М.: Энергоиздат,1982
Дополнительная литература
Теоретические основы электротехники, т.1,2, под ред. П.А. Ионкина
М.: ВШ, 1978
2. Кузовкин В.А. Теоретическая электротехника. – М.: Логос, 2005.- 480 с.
3. В.Ю. Ельникова, В.П. Кочетков Теоретические основы электротехники.
Электрические цепи, учебное пособие,ч.1,2. А.: Март,2002
Сборник задач по теоретическим основам электротехники/ Л.А.Бессонов, И.Г. Демидова и др.
М.: ВШ, 1988

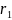 ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом