
РГЗ 5, 20 вариант
.docxПереходные процессы в линейных электрических цепях
Для исходной схемы цепи рассчитать классическим методом ток i1(t) после поочередного включения рубильников.
Построить график зависимости i1(t), учитывающий все коммутации.
Указания
Рубильники включаются последовательно в соответствии с указанными на схеме номерами через τ секунд.
При возникновении апериодического процесса τ =1/Р1, где Р1 – корень характеристического уравнения причем [P1]<[P2].
Исходные данные
Таблица 1
R1, Ом |
R2, Ом |
R3, Ом |
L, мГн |
С, мкФ |
E, B |
0 |
0 |
50 |
125 |
230 |
100 |

Рис.1 – Исходная схема
1 коммутация

Рис.2 – Схема 1 коммутации
Направление
расчетного тока будет рассчитываться
по следующей формуле:
До коммутации цепь от источника отключена, поэтому:
 .
.
Согласное законам коммутации независимые начальные условия будут:
 Определим
одно зависимое начальное условие,
которое потребуется при определении
постоянных интегрирования.
Определим
одно зависимое начальное условие,
которое потребуется при определении
постоянных интегрирования.
 ;
;
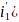 ;
;
Рис.3 – Схема после 1 коммутации
При
постоянном источнике
 в установившемся режиме емкость
представляет собой разрыв. Поэтому
значение
в установившемся режиме емкость
представляет собой разрыв. Поэтому
значение
 .
Следует отметить, что
.
Следует отметить, что
 и
и
 В.
В.

Рис.4 – Расчетная схема для нахождения характеристических корней уравнения
Для составления характеристического уравнения рассмотрим Рис.4 и запишем уравнение:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Корни характеристического уравнения:
 ;
;
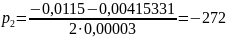 ;
;
Поскольку
оба характеристических корня действительные
отрицательные числа, при условии, что ,
будет апериодический процесс.
,
будет апериодический процесс.
Тогда
выражение свободной составляюще тока
будет иметь следующий вид:
Для
определения постоянных интегрирования
 и
и
 составим
уравнения:
составим
уравнения:

После
нахождения начальных условий
 ,
по
законам Кирхгофа и законам коммутации,
для схемы после коммутации, а также
расчетов принужденной составляющей
,
по
законам Кирхгофа и законам коммутации,
для схемы после коммутации, а также
расчетов принужденной составляющей
 и её производной
и её производной
 могут
быть определены значения
и
:
могут
быть определены значения
и
:

 ;
;
 ;
;
Решив уравнение получаем следующие значения:
 ,
,
 .
.
Выражение свободной составляющей будет:
 ;
;
Окончательно
получим полное значениепереходного
тока
 :
:
 ,
А
,
А
Запишем выражение для напряжения:

 ;
;



Рис.5
– График зависимости
от

2 коммутация

Рис.6 – Схема 2 коммутации
Запишем время замыкания второго ключа:
 c.
c.

Рис.7 – Схема после 2 коммутации
После
второй коммутации, как и после первой,
вначале проведем расчеты тока
 .
.
 ;
;
А

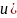

Согласно
законам коммутации независимые начальные
условия в момент
 после
второй коммутации
после
второй коммутации
В
Тогда определим ток :
А
Т.к.
в момент коммутации при
 начальные условия являются независимыми,
т.е.
,
начальные условия являются независимыми,
т.е.
,

Принужденная
составляющая искомого тока
 определяется
по Рис.7. При постоянном источнике
определяется
по Рис.7. При постоянном источнике
 В будет
В будет
;

Рис.8 – Расчетная схема для нахождения характеристических корней уравнения
Для составления характеристического уравнения рассмотрим Рис.8 и запишем уравнение:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Значение
характеристического корня:

Выражение свободной составляющей принимает следующий вид:

Определим постоянные интегрирования по начальным условиям:

Полное
значение переходного тока
 после второй коммутации будет:
после второй коммутации будет:




Рис.9
– График зависимости
 от
-
от
-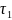
Список использованных источников
Асанов Т.К. Переходный процесс в линейной электрической цепи при нескольких коммутациях: Методические указания.- М.: МИИТ, 2004,-37с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи: учебник / Л. А. Бессонов. – 11-е издю., перераб. и доп. – М.: Гардарики, 2007. – 701 с.
Иванова С.Г., Теоретические основы электротехники. Расчёт линейных электрических цепей: учеб. пособие. – 2-е изд., перераб. И доп. / С.Г. Иванова, Ю.С. Перфильев. – Красноярск: ИПЦ КГТУ, 2006. – 312
